Métrologie des châteaux: le château des Allymes

1. Introduction

Nous avons déjà fait le tour de l'état actuel de la connaissance sur les châteaux du XIVème siècle, montré l'importance des nombres par leurs récurrences, et montré que les anciens avaient les moyens de cartographier leur espace en distances et en altitudes sur Ambérieu en Bugey.

Nous proposons maintenant un article sur les unités de mesures que les anciens du XIVe siècle ont utilisé, de manière non exhaustive. En effet, le mètre n'est pas censé exister au Moyen-âge et différentes unités avaient cours: la toise, la canne, le pan, la perche, l'aune, le pied, le pouce.

La toise au XIVe siècle équivaut à la canne qui vaut 6 pieds, de manière générale. On trouve parfois des toises de 5,5 pieds (Queyras) ou de 7,5 pieds (Ain).

Le pied équivaut au pan (Nice) et contient 12 pouces. 1 pouce = 12 lignes et 1 ligne = 12 points

Au XIVe s. , on compte donc par exemple: 18 Toises 5 pieds et 10 pouces. Pour les angles, sont utilisés les degrés/minutes/secondes du cercle à 360°. Les nombres décimaux sont introduits plus tard au XVIe s. par Simon Stevin puis Bartholomäus Pitiscus et John Napier.

La mesure du XIVe siècle peut donc se voir comme une suite géométrique de raison 12. C'est vrai aussi à la renaissance et pendant l'Ancien Régime précédant la mise en place du système métrique à la révolution.

Pour aller vite et passer les rébarbatifs paragraphes 2 à 4, voici leur résumé:

Il existe une standardisation en Savoie sur une toise de 1,875m=3×5/8 de 6 pieds de 3,125dm=25/8.

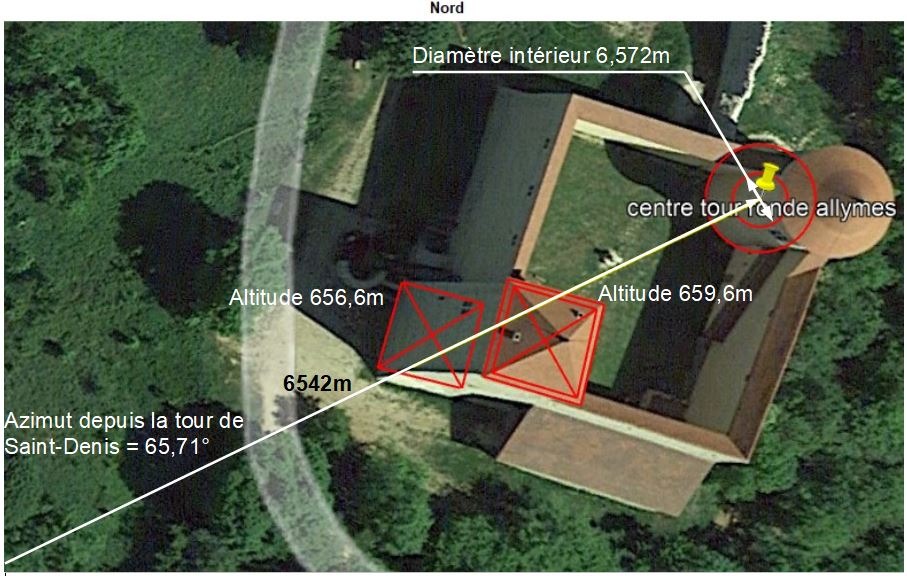
Il existe un rapport direct entre la toise delphinale de 2,046m et la toise Savoyarde. Ce rapport vaut la 6ème partie de 6,542 exactement, nombre que l'on retrouve souvent sur Ambérieu-en-Bugey. L'étude sera menée au château des Allymes avec ces toises car possédant un rapport d'espace géographique ET un rapport de nombre avec les 2 toises.

2. Le standard de la toise, mesure de longueur d'Amédée V de Savoie (1285-1323) selon A. Kersuzan¹,²

En Savoie, avant 1612, la toise variait entre 1,727 mètre et 2,512 mètres¹. Chaque localité avait son unité de mesure ou son système de mesure et l'on retrouve leur utilisation dans les comptes (recettes et dépenses) des châtellenies du comté puis Duché de Savoie.

Pour construire au XIVe siècle, un cahier des charges précis est fixé par un maître d'ouvrage (un Comte, un Duc ou un châtelain pour édifier le châteaux, les membres du chapitre pour édifier une cathédrale). Un maître d'œuvre a la charge de vérifier l'exécution du chantier pour atteindre l'objectif architectural recherché (les seigneurs locaux). Les maîtres, valets (compagnons) et apprentis de chaque métier ont la charge d'exécuter. Il en découle des délais à tenir, des besoins humains et matériels à définir, des études de sites et des solutions techniques à retenir¹,². Qui finance? le châtelain, sur place, nommé par le Comte possède des droits de recette sur la population (cens et taille, mais aussi recettes sur la justice) et les marchandises. l'argent sert à: payer une rente au châtelain, construire et/ou entretenir la construction, faire la guerre Delphino-Savoyarde.

Au château de pont d'Ain, l'auteur cite des murs de 4 pieds de 1,25m d'épaisseurs, donc 1 pied de 0,3125m¹,² . Et il conclue: "La toise utilisée à Pont-d'Ain était donc bien celle "à la mesure du seigneur" à 1,88m¹. En réalité, cela fait 1,875m si 4 pieds font 1,25m.

Il retrouve aussi, dans les comptes de la châtellenie, 111 toises pour faire 3 murs sur 4 de la grande salle (le 4ème est une courtine). Chaque mur est sur 3 rangées. Et effectivement en mesurant sur site l'auteur retrouve la valeur au sol, en mètre, de 111 toises divisée par 3 (car 3 rangées) pour une toise de 1,88m. Cela fait donc 37 toises au sol. Les comptes confirment les 3 hauteurs de toise et l'archéologie donne une valeur de plus ou moins 2,5 toises de hauteur pour chaque toise linéaire soit plus ou moins 4,8m¹.

Aucune trace d'un étalon n'a encore été trouvé pour le comté de Savoie. En général, une canne graduée jouait ce rôle. Le comte et les châtelains pouvaient très bien en avoir une, ainsi que les maîtres artisans¹.

La toise et le pied sont utilisées comme mesure technique et économique pour la facturation de la matière et de la valeur ajoutée par les maître-maçons et être consignés dans les comptes de châtellenie qui seront vérifiés par le comte. Ces mesures ont un rôle pratique de normalisation dans le comté, autant pour construire que pour financer la construction¹.

Nous ne pouvons qu'apprécier que l'auteur ait pris le soin de mesurer sur le château de base du XIVe pour en retrouver une valeur correspondant effectivement aux comptes de la Châtellenie de Pont-d'Ain du XIVe (aussi).

En conclusion, une toise savoyarde à 1,88m pour 6 pieds de 0,3133m ou bien une toise de 1,875 pour 6 pieds de 0,3125m. A déterminer.

On peut aussi ajouter que dans sa conclusion, A. Kersuzan mentionne les liens du Comté de Savoie avec le royaume d'Angleterre et le Duché d'Aquitaine depuis la fin du XIIe siècle, qui ont largement inspiré l'organisation et l'administration savoyarde¹. Il pose la question de savoir s'il en a été de même pour la standardisation des mesures. Cette remarque mérite qu'on s'attarde dessus tellement elle est importante pour la métrologie historique et donnera lieu à une publication ultérieure.

3. Les valeurs de longueur de la toise Delphinale

Aucun travail, à ma connaissance, ne montrent une standardisation de la mesure en Dauphiné comme A. Kersuzan l'a fait en Savoie. En effet, la qualité de la tenue des comptes de châtellenie et l'exhaustivité des détails fournis dedans, en Savoie, permet d'effectuer ce travail. En Dauphiné, les comptes sont beaucoup plus laconiques.

Thérèse Sclafert donne une canne (équivalent de toise) de 6 pieds et 8 pans valant 1,302m dans l'Embrunais et le Gapençais, donc dans le Haut-Dauphiné³. Cependant cela date de la mise en place du système métrique comme correspondance au XVIIIe s. .

Nathalie Nicolas donne une toise Delphinale à 2,046m, contenant 6 pieds de 34,1 cm⁴ , issue des comptes de la châtellenie de Briançon (1393-1394). Ceci correspond exactement aux valeurs de la toise Delphinale de l'époque de la conversion de 1790 et la mise en place du système métrique pour le département de l'isère⁵. Elle trouve aussi dans les comptes de 1336 de la châtellenie de Château-Dauphin (Italie) la toise de Chateau-Queyras et de Chateau-Dauphin qui vaut 1,8755m contenant 5,5 pieds de 34,1cm⁴. Cette valeur correspond à la toise standardisée de Savoie vue plus haut. De plus, "La canne (la toise) varie de 1,87m (Château-Ville-Vieille et Guillestre) jusqu'à 2,05m (Embrun, Chorges et Saint Firmin)".

Nicolas Payraud dans sa thèse trouve à Chateau-Queyras une toise à 1,875m⁶:

"[...] En 1339, ce donjon est un bâtiment carré de 4,75 toises de côté (8,90 m), comprenant trois étages sur 8,5 toises de hauteur (15,90 m)[...]".

A l'époque de la mise en place du système métrique, à Embrun, l'aune de 5 pans vaut exactement 1,25m et la toise 8 pans donc 2,001m⁷. Le système métrique semble corriger très légèrement celui d'Embrun. On remarque que l'aune de 1,25m de 5 pans d'Embrun du XVIIIe siècle, c'est comme 4 pieds standardisés de Savoie de 31,25cm du XIVe siècle.

En conclusion pour le Dauphiné de Viennois:

Une toise appelée toise Delphinale est répandue en Dauphiné à l'époque de la mise en place du système métrique: elle vaut 2,046m. Une Toise de 2,046m de 6 pieds se retrouve sur Briançon au XIVe siècle et que l'on retrouve presque à Embrun, Chorges et Saint Firmin (2,05m).

D'un autre côté, nous avons dans les comptes du XIVe siècle en Queyras une toise de 1,8755m contenant 5,5 pieds de 34,1cm.

On constate donc qu'en Dauphiné aussi, la Toise de 1,875m a été utilisée au XIVe siècle, comme en Savoie à la même époque, en particulier dans les localités frontières.

Mais l'aune d'Embrun (1,25m) datant du système métrique nous rappelle que la toise d'Embrun vaut 2m quasiment tout pile et rappelle le pied de Savoie de 31,25cm issu d'une toise à 1,875 (XIVe siècle). Un lien semble donc exister entre le mètre (1799), la Toise d'Embrun (Ancien régime), l'Aune d'Embrun (Ancien régime), et le pied de Savoie (XIVe siècle).

4. Rapport entre la toise delphinale et la toise Savoyarde

Toise savoyarde = 1,875m et sa fraction simple vaut 3×5/8 m (met en œuvre les 3 premiers nombres premiers 2, 3 et 5)

pied de savoie=31,25 cm et sa fraction simple vaut 5×5/8 dm (ne met en œuvre que 2 nombres premiers 2 et 5)

Faisons le rapport entre la Toise Delphinale et la toise savoyarde:

Rapport=2,046/1,875=1,0912 dont la fraction simple vaut 4×3/11 exactement, et qui représente la 6ème partie de 6,545 exactement. Ce nombre est retrouvé systématiquement sur l'axe tour de Saint-Denis/Allymes sous plusieurs formes.

Il en résulte que la fraction rationnelle de la Toise Delphinale = 45/22=(5×3³)/(2×11) m (met en œuvre 4 nombres premiers 2, 3, 5 et 11)

Cette forme de fraction est plus complexe à utiliser que celle de la toise de savoie.

Conclusion

Deux unités importantes d'un même espace géographique, au XIVe siècle, sont liées par une mise en produit de puissance de nombres premiers DANS LE SYSTEME METRIQUE.

Utilisons la valeur de la toise à 1,875m au château des Allymes à Ambérieu-en-Bugey, puisqu'elle est retrouvée en Savoie ET dans le Queyras Delphinal, et que le rapport de la toise savoyarde à la toise delphinale est un nombre déjà présent entre la tour de Saint Denis et le château des allymes: 6542.

5. Métrologie au Château des Allymes: les superficies identifiables

Pour les superficies, on peut remarquer que les aires marquant des surfaces géométriques clairement identifiées renvoient à des nombres marquants:

• La surface au sol de l'enceinte fortifiée ceinturée des 4 courtines forme un carré de 36m de côté. Soit une surface de 1300m² environ;

• L'aire marquée par le centre des 3 tours et l'angle nord de la muraille légère ("coin") vaut 5000m².

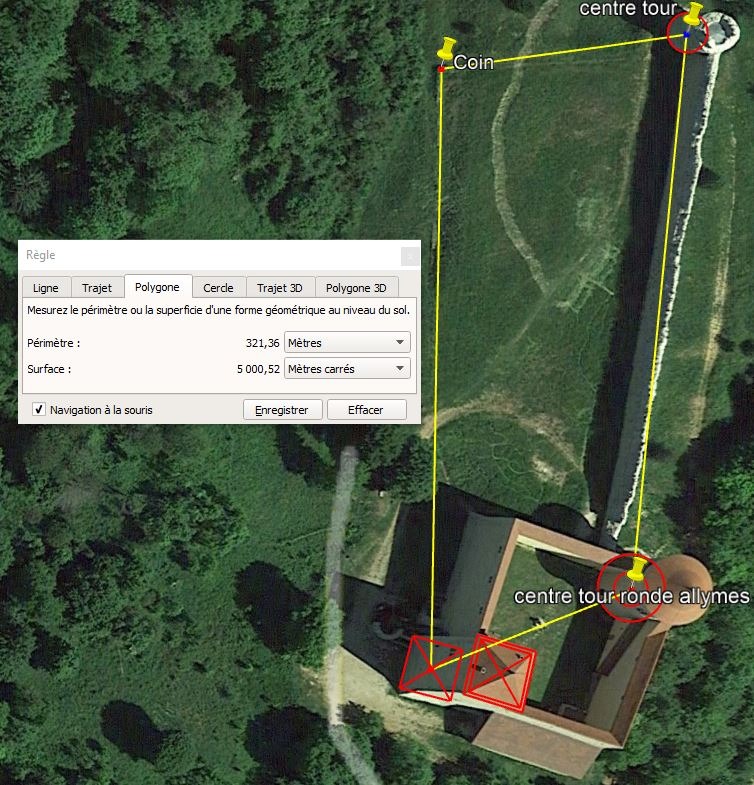
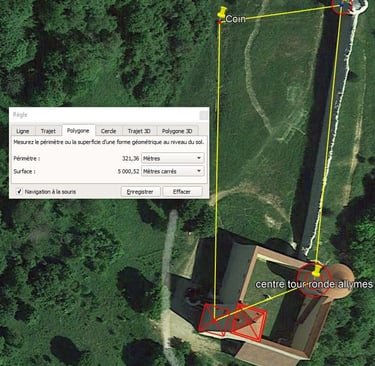
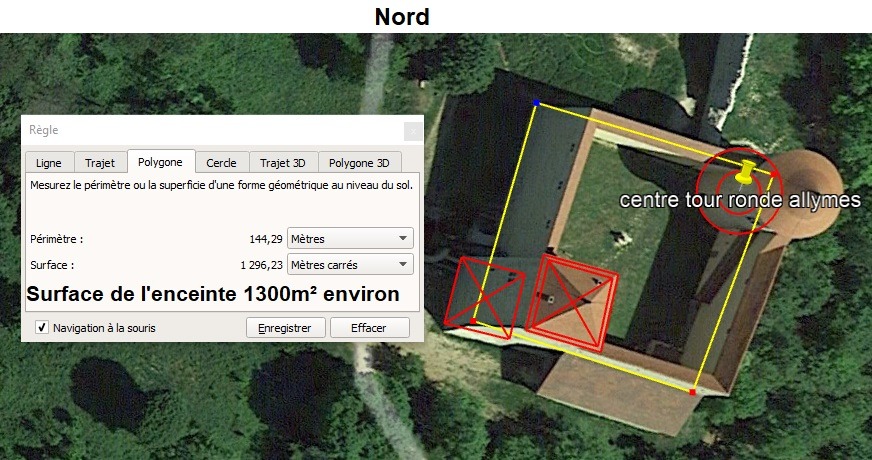
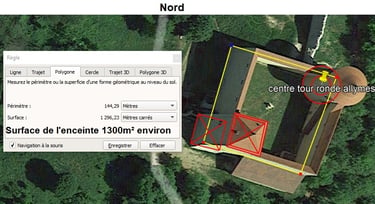
a. La combinaison du nombre 65

Nous avons déjà ciblé dans un article précédent que le nombre 65 est fréquent concernant pour l'axe Tour de Saint-Denis / château des Allymes. Ceci est vrai pour les distances, les altitudes, l'azimut ainsi que pour les dimensions du château.

Or nous avons deux superficies marquant le 5 et le 13.

Mais 5 et 13 forment 65 par leur produit , justement

Rajoutons une dimension de la tour ronde liée à 65:

Le rayon extérieur de la grande tour ronde fait 6,05m EXACTEMENT.

Le nombre structure ainsi la configuration des 2 châteaux, mais est aussi présent dans la structure.

c. Et si la superficie était en Toises carrées?

Une Toise savoyarde carrée = 1,875² = 3,51563 en mètres².

5000/3,51563=1422,22 Toises savoyardes carrées

1296/3,51563= 368,64 Toises savoyardes carrées

Il est difficile de retomber ET sur des nombres de la suite de Fibonnacci, ET sur des nombres premiers simples comme le 5 et le 13, ET surtout sur la correspondance des distances et des altitudes et des azimuts et des architectures déjà constatée dans un autre article avec le nombre 65.

Autrement dit:

5000×1300=6,5 . 10⁶ en m² et cela correspond à ce que l'on a par ailleurs avec le nombre 65 en m sur les distances, altitudes, azimuts et architecture. Les nombres sont "liés".

MAIS en Toises carrées

1422,22 × 368,64=5,243 . 10⁵ Toises carrées mais les distances tour carrée de Saint Denis et Tour carrée Allymes ne correspondent pas ( = 3466,66 Toises). Idem pour les altitudes, azimuts (qui lui reste un nombre de 65,7°N) et architectures. Les nombres sont "déliés."

d. Synthèse

Des nombres entiers de mètres carrés (5000 et 1300), affichant des nombres premiers, qui plus est de la suite de Fibonacci, et qui plus est en redondance avec les nombres en mètres des distances, azimuts dimensions architecturales est un indicateur de l'utilisation certaine du mètre dans les monuments.

Nous allons, dans la partie suivante, étudier les distances délimitant ces deux surfaces.

b. La suite de Fibonacci

Leonardo Fibonacci (vers 1170 - vers 1250) était un mathématicien Italien. Il a contribué à l'utilisation des nombres Indo-arabes en Italie (1,2,3,4,5,6,7,8,9,0) remplaçant le traditionnel système de notation romain.

Une suite, dite suite de Fibonacci, lui est attribuée. Tout nombre issu de la suite initialisée à 0 et 1 est le résultat de l'addition des 2 termes précédents:

F(n-2)+F(n-1)=F(n)

soit:

0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 etc...

Propriété: Le rapport entre F(n) et F(n-1) tend à former le nombre d'or 1,618 lorsque l'on va dans le sens croissant.

Le nombre d'or est aussi appelé divine proportion. Toute chose formée à tendance à converger vers ce nombre en proportion (nature, architecture, etc...)

Propriétés du nombre d'or:

• 1,618²=2,618

• 1/1,618=0,618

Or les 2 surfaces balayés montrent deux nombres de cette suite:

5 et 13

C'est à dire F(5) et F(7)

6. Concevoir un "château des Allymes"

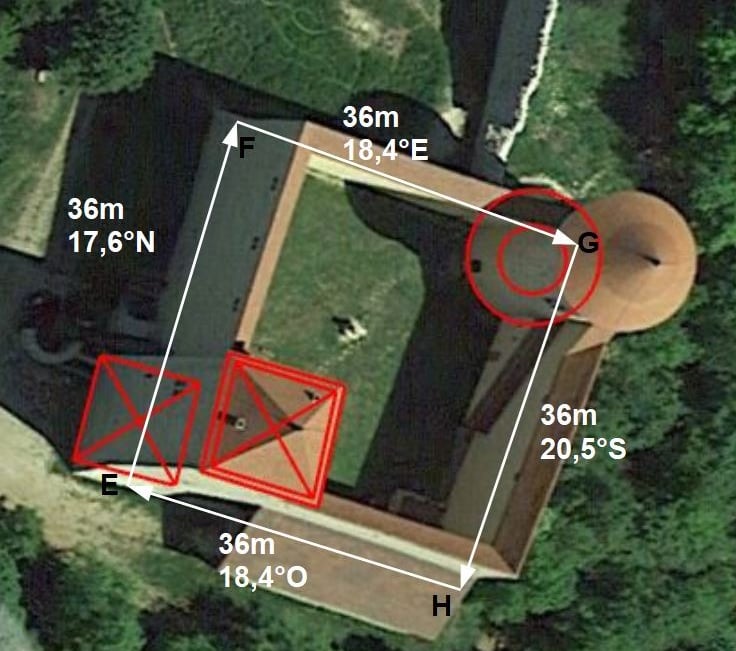
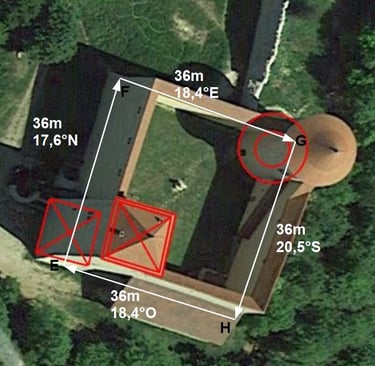
Etudions les longueurs et azimuts des 4 points caractéristiques des deux enceintes quadrangulaires en mètres et en ° (les 36m de côté de l'enceinte EFGH sont donné par les archéologues L. d'Agostino, et E. Chauvin-Desfleurs).

Les multiples de 6 ou 12 sont évidents pour les deux enceintes:

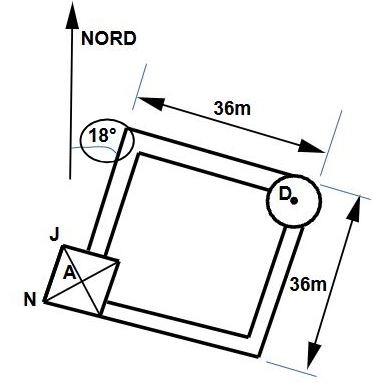
Pour l'enceinte ABCD, on a d'abord un plein nord sur 120m. On a ensuite un -6° par rapport à l'est. Puis on a un +6° par rapport au sud (6°S). Enfin on a une distance de 7×6 m en diagonale.

Pour l'enceinte EFGH, nous avons 6×6 m de côté. De plus la moyenne des angles relevés pour l'orientation des courtines tourne autour de 18,2°±0,5°, si on néglige l'influence de la mesure de 20,5°S qui semble s'écarter. L'enceinte est donc dirigée à +18°N.

Pour remarque, l'épaisseur des courtines fait 2,4m........ soit 6×4 décimètres.

Pour autre remarque, la hauteur des courtines depuis la cour intérieure fait, sous le toit......12m de haut. Rappelons nous aussi que A. Kersuzan et les archéologues parlent d'une hauteur de plus ou moins 4,8m par toise linéaire (multiple de 12).

Le diamètre extérieur de la tour ronde mesure?....je laisse au lecteur le soin de faire l'expérience en allant sur place pour mesurer ce diamètre extérieur sous les combles de celle-ci.

On peut donc maintenant clairement prendre au sérieux l'importance du mètre là dedans, tout en ne négligeant pas les toises vues précédemment car elles ont un lien fractionnaire avec elles. En effet, les comptes de châtellenies sont clairs. On construit et on paie les murs en toises.

En Toises Delphinales (TD), que cela donne-t-il? des nombres irrationnels déconnectés de la division par 6.

Pour l'enceinte ABCD, on a d'abord un plein nord sur 58,651 TD . [...] . Enfin on a une distance de 20,5279 TD en diagonale.

Pour l'enceinte EFGH, nous avons 17,5953TD de côté. [...]

Pour remarque, l'épaisseur des courtines fait 1,173TD.

Pour autre remarque, la hauteur des courtines depuis la cour intérieure fait, sous toit......5,8651 TD de haut.

Et en Toises de Savoie (TS) ? nous obtenons des "centi-toises", faciles à mesurer en système décimal, mais sur une toise déjà divisée en 6 pieds.

Pour l'enceinte ABCD, on a d'abord un plein nord sur 64 TS . [...]. Enfin on a une distance de 224/10 TS en diagonale. "donc au dixième"

Pour l'enceinte EFGH, nous avons 192/10 TS de côté. [...] ."donc au dixième"

Pour remarque, l'épaisseur des courtines fait 128/100 TS. "donc au centième"

Pour autre remarque, la hauteur des courtines depuis la cour intérieure fait, sous toit......64/10 TS de haut."donc au dixième"

Conclusion

La division en toise Delphinale de 2,046 propose des nombres irrationnels pour la construction. Les nombres ne sont pas des multiples de 6, alors que nous avons vu l'importance de la redondance de ce nombre, au moins dans le système métrique.

La Toise de Savoie, en revanche est assez cohérente en construction pour le château des allymes. Il s'agira juste d'aller au dixième voire au centième de Toise de Savoie près, soit 1,875cm. On peut tout à fait graduer une toise en 100 parties, par exemple. De plus, les longueurs grandes échelles seront soit en nombre entiers, soit en entier plus 1/3 ou 2/3 de Toise savoyarde, c'est à dire un nombre entier de pied. C'est possible, et facile.

Nous avons donc une utilisation du mètre en nombres entiers (le plus souvent), avec des multiples fréquents de 6 (ou 12). Cela rappelle évidemment les subdivisions médiévales: 1 toise = 6 pieds = 12×6 pouces =12×12×6 lignes=12×12×12×6 points.

On constate aussi que, comme dans le Queyras ou Château-Dauphin, aux Allymes aussi en Dauphiné au XIVe siècle, une toise de 1,875m a tout à fait pu être utilisée. A l'interface Savoie/Dauphiné, à cette époque, nous avons par ailleurs Pont-d'ain pour laquelle une toise à 1,875 ou, du moins, à 1,88 est utilisée.

Cependant, l'implantation est métrique car le code est en nombres entiers de mètres ET le plus souvent multiples de 6 en longueur et azimuts à la fois ET se retrouvant aussi sur une simple épaisseur de courtines ou diamètre de tour ronde. Nous n'avons que très peu d'information sur les architectes, dans les comptes des châtellenie, en général. Intéressons nous maintenant à: qui a réalisé l'édifice et comment cela a-t-il pu être fait.

7. Essai d'implantation du château sur les quadrilatères ABCD et EFGH

Le travail d'implantation géométrique ne rapportant rien par définition, il est probable que l'architecte soit le Prince (Dauphin de viennois), le châtelain (nommé par le Prince) ou un fidèle, quelqu'un de très cultivé en tout cas, pour jouer avec les nombres et la géométrie terrestre et avec référence cardinale. Il faut avoir eu les moyens financiers et du temps pour accéder au savoir vu précédemment. Le coût d'une telle étude géométrique à planter correctement 8 piquets, étude initiale, étant la satisfaction d'avoir conçu l'œuvre géométriquement avec un plan, un compas, une équerre. Nous avons vus que les "grands" du monde du XIVe siècle étaient, pour beaucoup, des gens mettant les arts libéraux issus de la Grèce au centre de leur éducation. En particulier les nombres, la géométrie, l'astronomie, et la musique. prenons en exemple Frédéric II Hohenstaufen empereur du Saint-Empire-Romain-Germaique au XIIIe s., mais aussi Humbert II (Dauphin de Viennois de 1333 à 1349).

L'élévation des murs, quant à lui, représente un coût financier énorme de maitrise, compagnonnage, apprentis, et ouvriers, et matériaux. Mais pour une valeur ajoutée certaine à la guerre.

Reconstituons maintenant l'enceinte quadrangulaire ABCD. Pourquoi elle en 1er? à cause de sa référence au Nord d'où vont partir les visées.

Un architecte plante un piquet en A qui sera futur centre de tour carrée (il peut aussi matérialiser la diagonale de la cour passant par les centres des tours, Saint-Denis, carrée Allymes, ronde Allymes). Il part plein nord sur 120m ou 64 TS (entier) et il plante un piquet B qui formera le coin extérieur. Il vise plein EST moins 6° et plante un piquet C à 51m (entiers...ou bien 27 Toises, 1 pied et 2,4 pouces). Il vise plein SUD plus 6° sur 110m (entiers....ou bien 58 Toises et 4 pieds) pour planter le piquet en D, avec une excellente mire réelle qu'est la tour de Saint-Denis au loin pour contrevérifier la diagonale entre les deux tours constatée dans un autre article.

Pour viser à 6°, découper un cercle en 60 parties de 6° est relativement aisé. On découpe le cercle en 5 au compas, puis en 15. Chaque partie peut être individuellement divisée en 2, puis en 2.

Sûrs de la diagonale passant par le centre des tours, ils ont pu tracer la courtine en plantant les 4 piquets EFGH des courtines tels que l'enceinte soit un carré au sol de 36×36 et orienté de 18° Nord ( division du cercle en 10, puis chaque partie en 2 pour viser à 18°N).

Voilà. Les points sont posés. Un autre article traitera un peu de la maçonnerie, dans laquelle la toise est utilisée non pas pour implanter, mais pour maçonner et facturer.

8. Conclusion

Le château des Allymes est une double enceinte quadrangulaire de multiples remarquables (2,3,4,6,12, etc...) sur les distances et orientations, ainsi que sur l'architecture. Il est positionné par rapport à la tour de Saint-Denis et cartographiée très précisément en altitudes, azimuts et distances sur une autre série de nombres remarquables issus de la suite de fibonnacci (le 5 et le 13) formant un nombre (65) omniprésents retrouvé dans l'architecture..

Comment retrouver un sens historique avec la métrologie?

Nous avons vu précédemment qu'un seul nombre peut être chaîné à deux châteaux: 65 suivi d'un 3ème voir 4ème chiffre significatif.

Nous avons vu que les 4 châteaux majeurs forment une carte à l'échelle 1:1 des distances, altitudes et azimuts (Cartographie et Cartographie2)

Nous avons vu que les multiples de 6 en nombre entier interviennent en permanence au château des Allymes dans l'unité métrique (Métrologie).

Enfin, nous avons proposé une méthode d'implantation du château des Allymes à partir de 8 points caractéristiques formant les 2 enceintes quadrangulaires (Métrologie).

Approfondissons maintenant le sujet de l'implantation et de la métrologie. En effet, il a bien fallu dimensionner et/ou positionner d'autres éléments....notamment les murs d'enceinte.

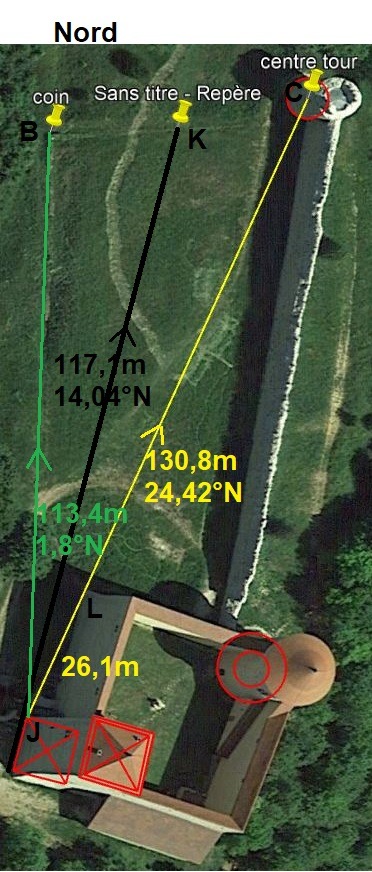
Voici des éléments à remarquer ou à interpréter pour positionner enceinte légère et courtines. Alors je vous laisse à Géoportail ou Google earth, ou mieux, à des mesures sur place et Je vous laisse le soin d'interpréter et nous regarderons ça après! (voir figure ci-dessous)

1. Le mur d'enceinte légère, partie JB

Voici ce qu'il reste du mur d'enceinte légère , observée depuis B vers le château.

Nous pouvons observer qu'un dispositif permettant de monter le mur droit sur plus de 110m a été mis en place entre le point B, coin de l'enceinte légère, et J, angle de la tour carrée.

Le coin nord ouest de la tour carrée a donc servi tout autant que le centre de la tour carrée pour monter l'édifice.

2. Le mur d'enceinte légère, partie JK

Observons maintenant le point K. Le point K est le milieu de l'enceinte légère nord. De ce point, rejoindre J signifie orienter la tour "carrée" dans ce sens. Nous avons un azimut de 14,04°N, cet angle est un angle caractéristique de la géométrie par modules carrés au sol. C'est la diagonale d'un quadruple carré orientée plein nord qui est utilisée.

Mais ce qui est très particulier dans cette géométrie de 127,4m orientée à 14,04°N, c'est qu'elle donne un module valant la seconde d'arc de méridien à la latitude d'Ambérieu-En-Bugey. Ceci représente donc les dimensions de la terre, ici à Ambérieu-en-Bugey.

De plus le coté nord de l'enceinte légère marque une inflexion vers la tour nord, à partir de ce point K.

3. Le mur d'enceinte légère, côté nord BKM

Remémorons nous la distance AB. Elle vaut 120m avec une direction plein nord.

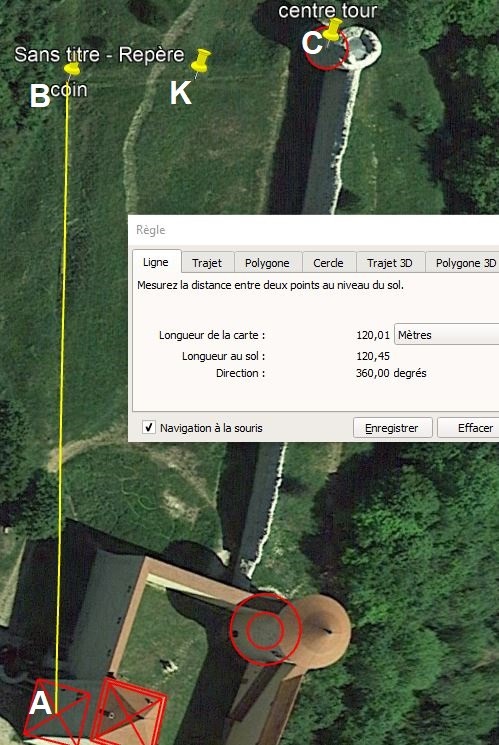
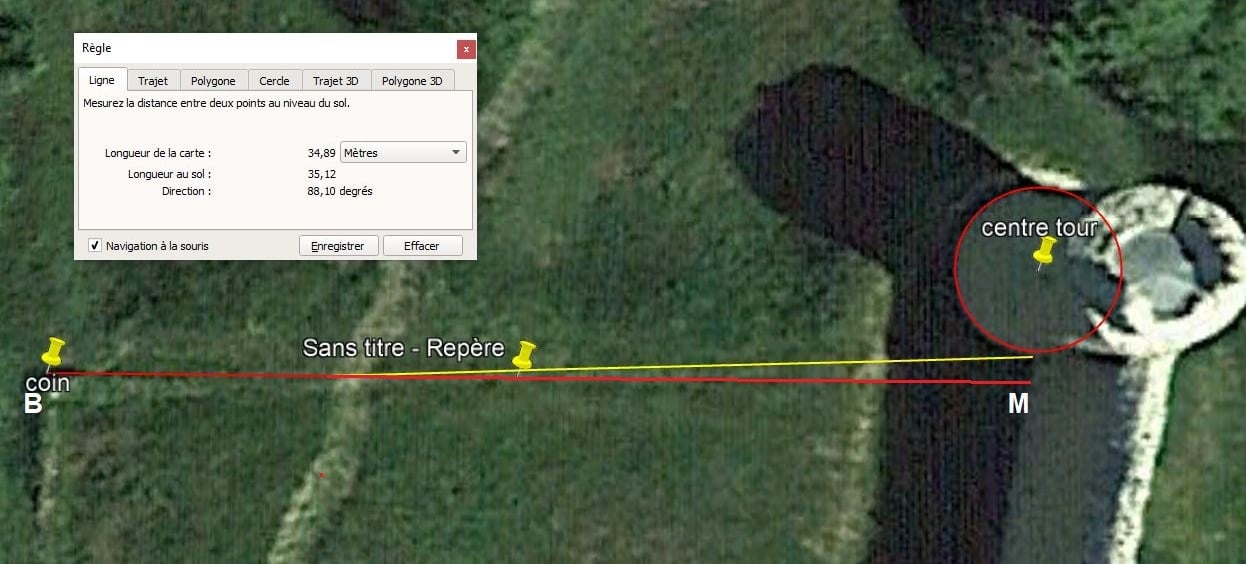
Une inflexion existe dans le mur côté nord....Cependant prolongeons le mur et orienté EST-OUEST et allons jusqu'à la muraille au point M. La distance vaut 50m.

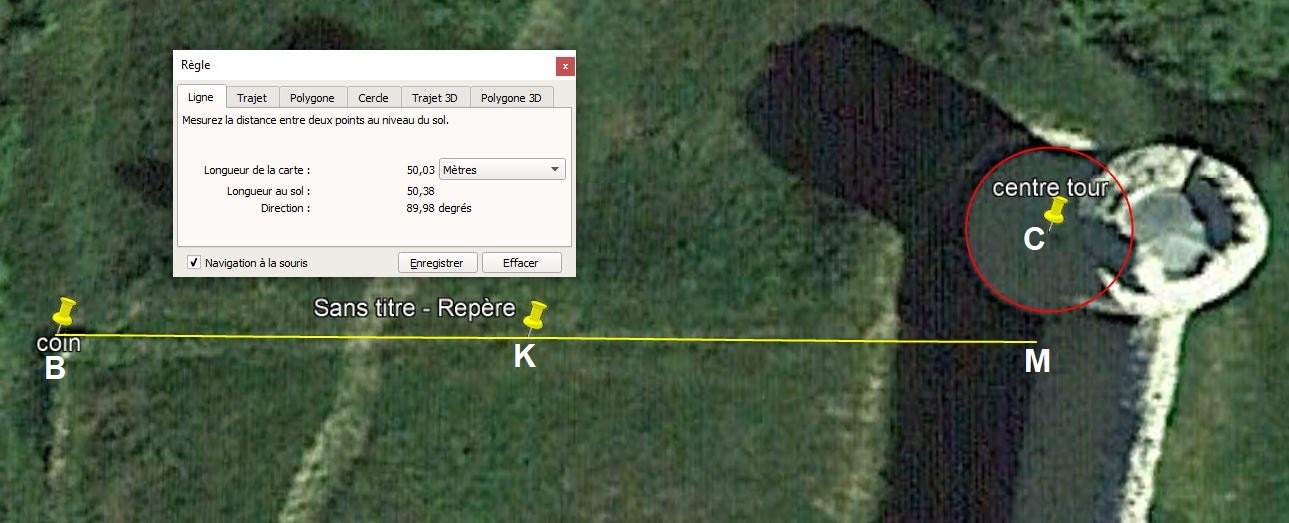
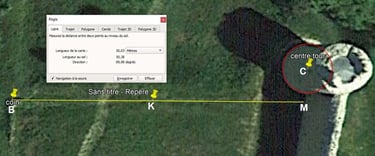
La première partie est plein Est. Le relevé des archéologues¹ montre aussi l'infléchissement mais voit le mur dirigé à l'Est - 3 ou -4°.

La distance BM est donc dirigée à 90°N, et elle suit la première partie du mur (en rouge) et la distance vaut 50m. Le triangle A B M est donc le 2ème triangle de pythagore. Voici une image depuis le coin B et l'on voit bien que le départ du mur, nettement dessiné, qui se dirge non pas vers l'angle de la tour ronde mais bien 1m à 1m 50 à droite. Pourtant au bout, la muraille jointe bien la tour ronde à l'angle.

Je conclue que le mur côté Nord possède bien 2 parties. Une première partie, la moitié, est orientée EST-OUEST. La deuxième partie s'infléchie pour aller cherche la coin de la tour ronde.

La question est : pourquoi donc?

Un article ultérieur en parlera. Il reste ici la géométrie du 5-12-13:

4. Comment la tour ronde nord est-elle positionnée?

Nous avons vu que AB= 120m exactement, et orienté plein nord.

Partons de J et allons plein nord en R. Recoupons avec un axe EST-OUEST pour revenir au point C, centre de la tour ronde Nord.

Constatations:

Se placer en J et regarder le point C (déjà implanté dans un autre article) permet de positionner L angle des courtines NORD-OUEST. L'angle de 24,42°N correspond à la diagonale d'un rectangle de 5 par 11 orienté plein nord dans sa grande longueur. Les points J, C et L sont alignés. Ici les nombres ne sont pas étonnants. 130,8 c'est 2 fois le 65,4, que l'on a pu observer maintes fois entre Tour de Saint-Denis vers château des Allymes (voir cartographie2).

La distance JL vaut environ 26m, mais difficile à mesurer précisément. JL≈ JC/5

Mais il y a quelque chose de plus dans cette géométrie, c'est le jeu entre le 11 et le 119 pour engendrer un rejeton du nombre d'or.

Le côté de 11 unités de la géométrie fait 119m.

Le côté de 5 unités de la géométrie fait 1190/ (2×11)m.

Mais 130,8 ≈ 1,1×119. Et le nombre d'or au carré divisé par 2 = 1309. Avec les modules de 5×11 avec le 119 de côté 11, nous obtenons une diagonale signifiante du nombre d'or au carré/2.

Chacun des côtés du triangle JRC possède une relation aux nombres 119 et 11. 11 et 119 forment le nombre d'or à leur manière dans la géométrie modulaire carrée de 5 par 11!

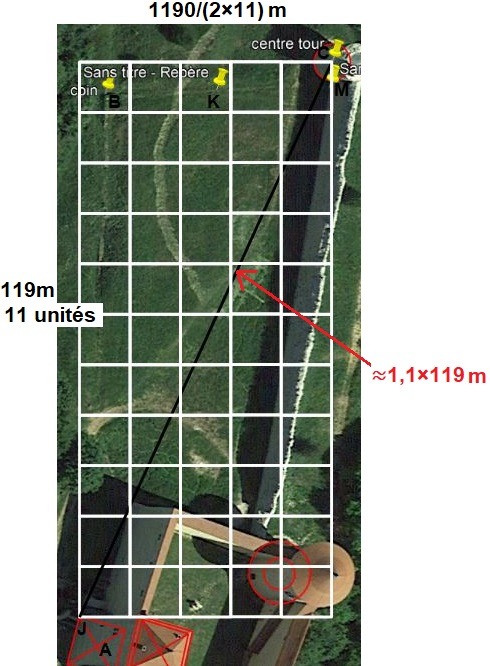
En conclusion, du point de vue de l'arpenteur-géomètre médiéval, se placer au point J de la tour carrée permet de positionner précisément le centre de la tour ronde avec une géométrie modulaire mesurable, dont les nombres indiquent leur importance dans la construction, et faisant ressortir un nombre bien connu au moyen âge: le nombre d'or.

Métrologie des éléments de structure

Nous avons vu en partie comment positionner les centres géométriques, points caractéristiques au château des Allymes, à travers les nombres, la géométrie, les références terrestres.

Nous allons maintenant étudier les dimensions des éléments de géométrie du château: tour carrée, tour ronde, enceinte principale, ....

1. Côté extérieur de la tour carrée

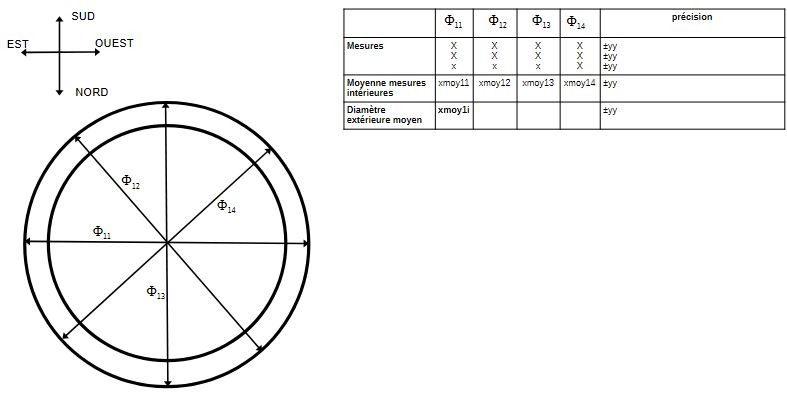
Idéalement, nous aimerions mesurer pour chaque section chaque côté plusieurs fois en faire la moyenne, puis faire la moyenne de toutes les valeurs pour avoir la meilleure idée de la valeur de ce côté. Les courtines, les constructions tardives, le manque d'ouverture empêchent ceci.

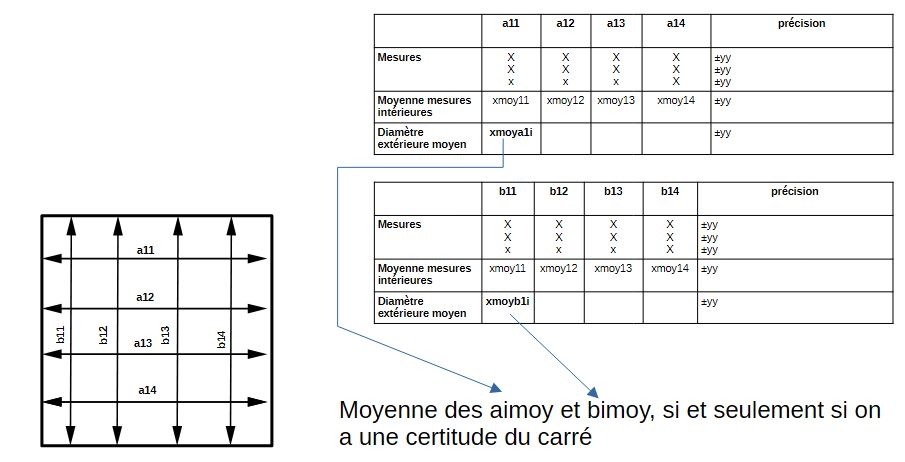
Nous avons 12 créneau au dernier étage, 3 par face et qui se font face. Nous avons mesurés 3 fois ls cotes a1, a2, a3 pour en faire une moyenne de chaque cote. Idem pour les cotes b. Nous avons aussi pris les cotes intérieures.

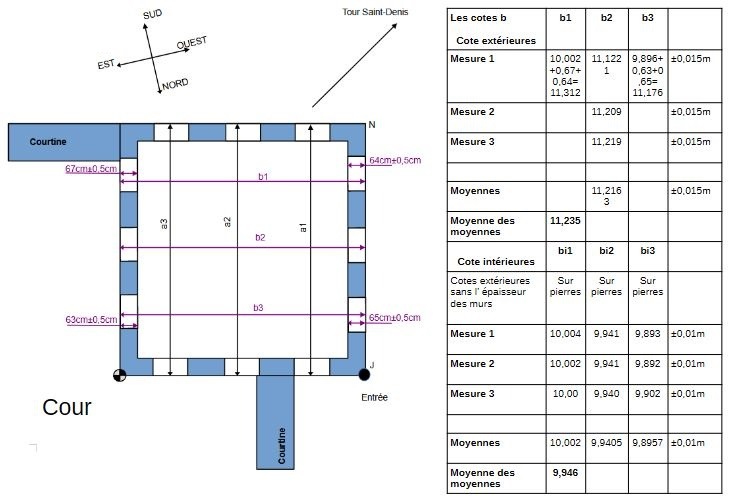
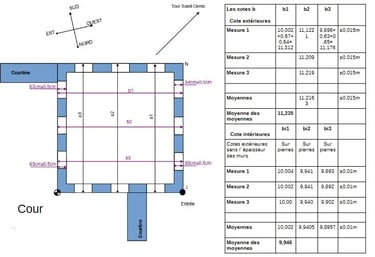
On peut remarquer que les cotes extérieures a comme les cotes b ne sont pas régulières, et évoluent de manière croissante (ou décroissante):

• a1<a2<a3;

• b1>b2>b3.

Mais nous remarquons aussi que a3=b3+ 11,18m

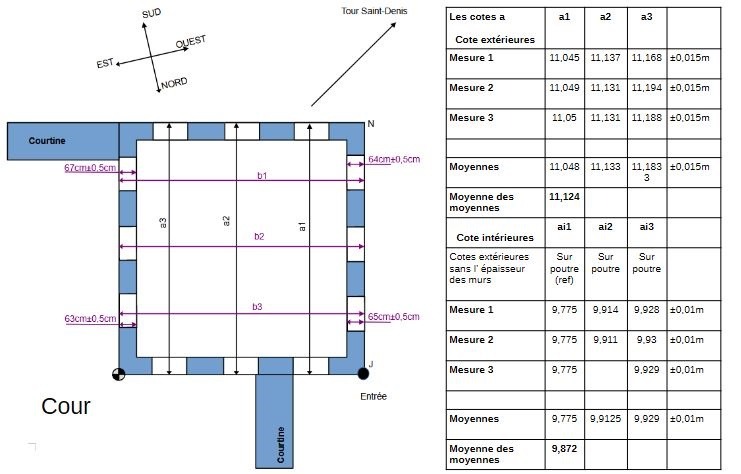
Faisons la moyenne de ces cotes.

Moyenne des cotes a=11,124m

Moyenne des cotes b=11,235

Il y a donc une différence de 11,1cm en moyenne entre les cotes a et b.

Faisons la moyenne de ces 2 cotés moyens= 11,18m. Or on a déjà vu que a3=b3+ 11,18m.

Ce nombre est bien connu puisqu'associé très souvent dans les structures de part le monde, à savoir la racine de 5. Ici, la racine de 125 = 11,18m.

Mais à ce stade, cela reste une hypothèse. Etudions la diagonale.

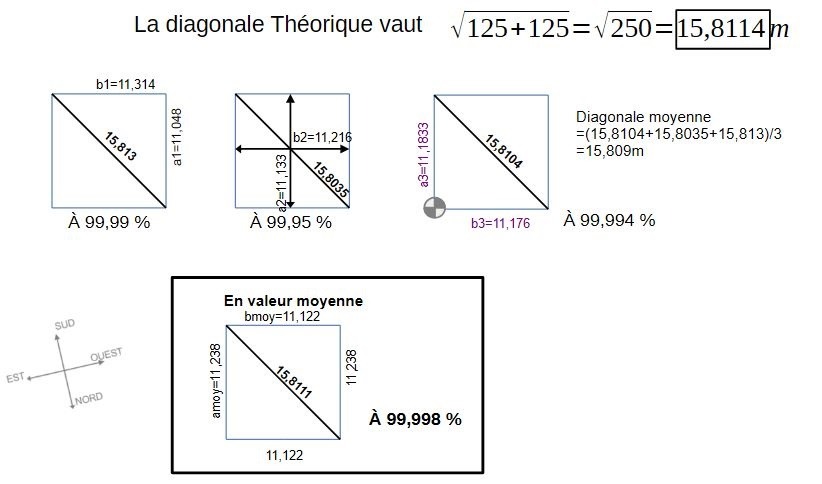
L'hypothèse d'un carré de coté racine de 125 implique la racine de 250 comme diagonale, soit 15,8114m.

Or, nous nous apercevons que pour les cotes qui s'écartent le plus de la valeur cible, a1 et b1, nous avons une racine de 250 quasiment exacte. idem pour a2 et b2, et pareil pour a1 et b1.

La cote de racine de 250 a été tenue tout du long par les constructeurs, même après le réaménagement du côté sud ouest.

En conclusion, nous avons bien un carré intentionnel de racine de 125 de coté.

D'autant que l'on put le vérifier avec les mesures photogrammétriques données par les archéologues Laurent D'Agostino et Evelyne Chauvin-Desfleurs. Par interpolation linéaire, nous retrouvons les valeurs mesurées au niveau des créneaux.

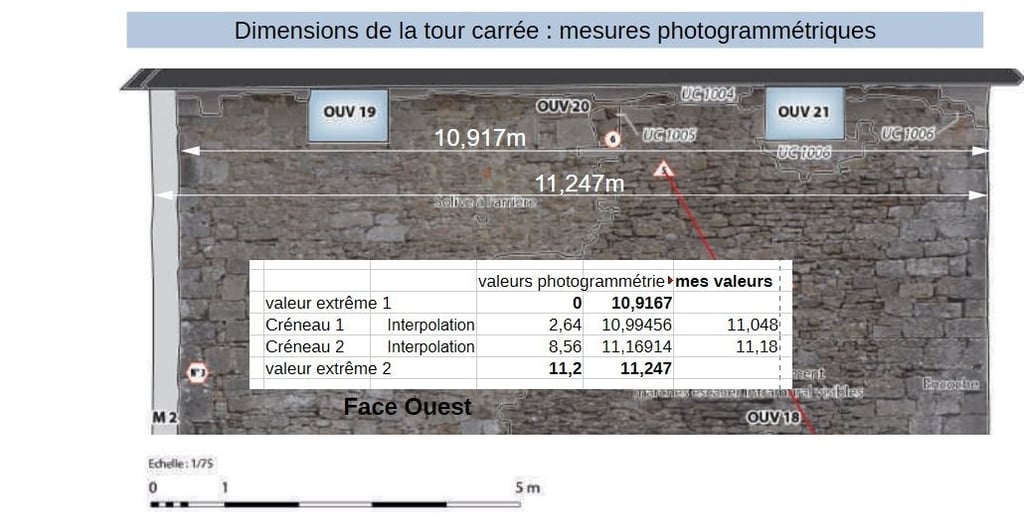
La tour carrée a donc un carré de coté racine de 125 intentionnel impliquant la racine de 250 comme diagonale.

Nous voyons ici que nos affirmations sur le mètre trouve de nouveau un écho, une confirmation. En effet, trouver un irrationnel comme la racine de 5, constitutive du nombre d'or, n'est absolument pas un hasard. En d'autres termes, changer d'unité ici enlève le rapport au nombre d'or.

Par ailleurs, nous pouvons ici calculée une superficie de construction:

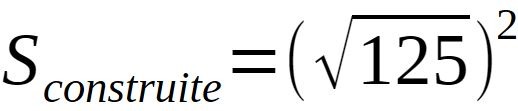
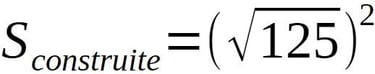
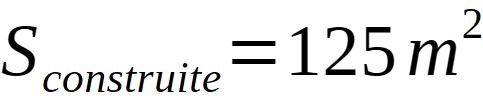
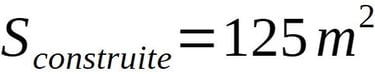
Ceci nous renvoie de nouveau à un nombre entier de mètres carrés, donc l'utilisation du mètre au XIVe siècle.

A remarquer, la racine de 125 est un irrationnel, et nous tombons sur une surface construite rationnelle en mètres carrés.

Le côté de la tour carré est donc un côté intentionnel de taille racine de 125, tout ça en mètres.

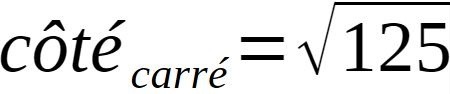
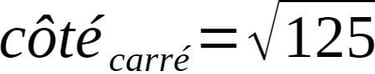
2. Côté extérieur de la tour ronde

Idéalement, nous aimerions mesurer pour chaque section chaque diamètre plusieurs fois et en faire la moyenne, puis faire la moyenne de toutes les valeurs pour avoir la meilleure idée de la valeur de ce diamètre. Les courtines empêchent ceci.

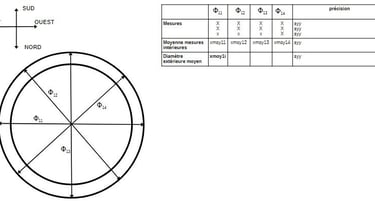
Puisque nous ne pouvons pas procéder ainsi, nous allons donc prendre les mesures que l'on peut prendre. Au dernier étage, il y a 4 ouvertures à 90° les unes des autres. Nous ne pouvons pas mesurer directement les cotes extérieures mais entre rebords. Puis on ajoute les rebords. Voici les relevés:

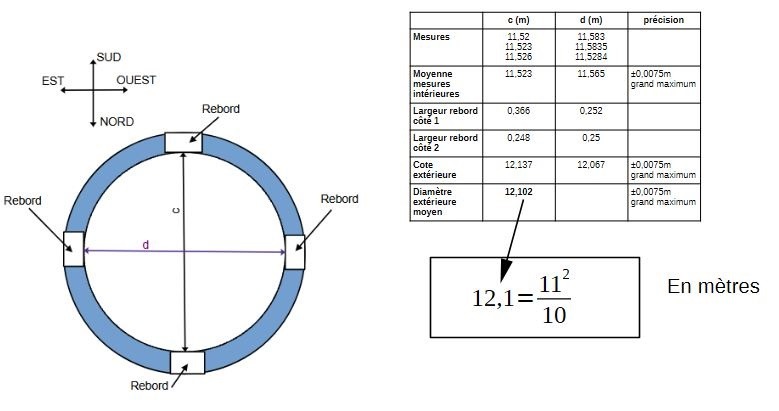
La cote moyenne totale est de 12,1m de diamètre.

Tant en cartographie, qu'en métrologie nous avons démontré que l'unité de mesure est le mètre. 12,1 en mètre est un nombre décimal. Son nombre fractionnaire est :

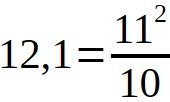
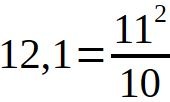
Nous avons vu que le nombre premier 11 intervient très fréquemment au château des Allymes. le plan modulaire carré au nord est un 5 par 11.

De plus la distance entre les centre des 2 tours rondes vaut 110mètres exactement.

Calculons maintenant la superficie construite à la tour ronde:

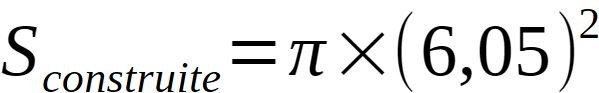
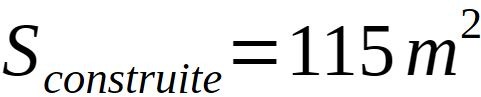
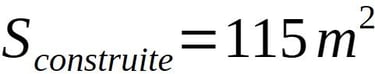
Voilà, même principe que pour la surface construite de la tour carrée.

On part d'un nombre décimal en rayon à mettre en superficie par l'irrationnel pi= 3,14159..... et l'on retombe sur un nombre entier de mètres carrés.

D'ailleurs, de la même manière que pour la tour carrée, le résultat est un multiple de 5.

En utilisant le rapport des archéologues, je me suis aperçu qu'avec les mesures photogrammétriques, les archéologues Laurent D'Agostino et Evelyne Chauvin-Desfleurs mesurent 11,8m pour le diamètre extérieur de la tour ronde. J'ai donc repris les mesures photogrammétriques.

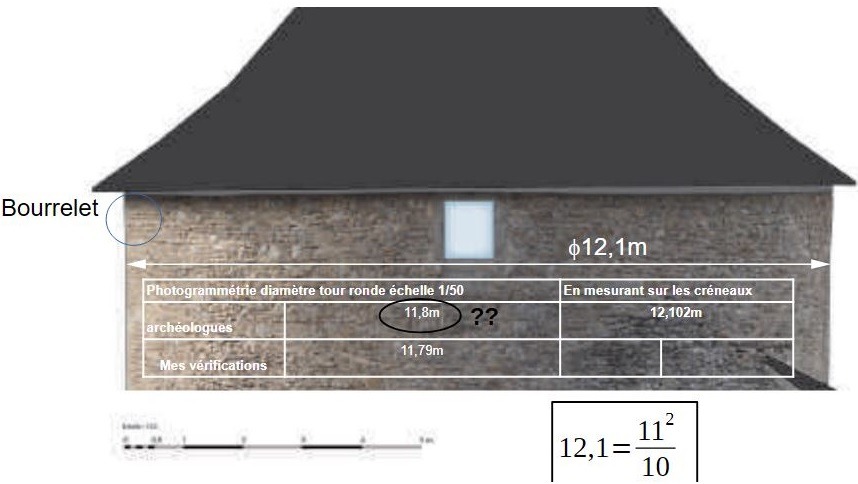
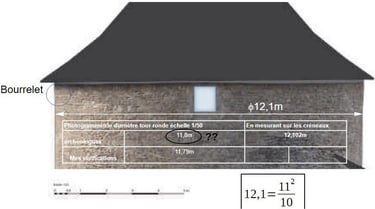
J'ai d'abord vérifié à l'endroit où je prends moi les mesures, combien le relevé photogrammétrique donne. Et il donne en effet 11,79m.

Il semble donc y avoir une erreur de 30 cm, au moins à l'endroit dont nous prenons, nous, les mesures.

En observant le relevé photogrammétrique, on observe un "bourrelet", mais il se trouve plus haut que l'endroit mesuré.

Etant sûr de la mesure que nous avons relevé:

• Soit l'endroit où nous avons pris les mesures est plus grand en diamètre, mais alors pourquoi ne le retrouve-t-on pas sur les mesures photogrammétriques?

• Soit des erreurs ont été faites en photogrammétrie.

Faute de plus d'informations, et puisque la mesure photogrammétrique à l'endroit où nous avons mesurée est contradictoire, je suis pour l'heure obligé de conclure à une valeur de 12,1m, qui existe bien sur le terrain.

3. Côté de la cour principale

L'archéologue Laurent d'Agostino précise que la cour principale carrée fait environ 36m de côté ⁹ . Il précise qu'elle fait 1296 mètres carrés de superficie.

Voilà ce que cela donne:

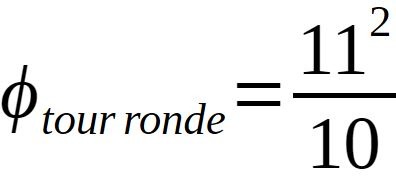
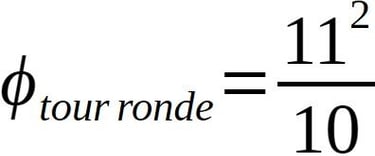
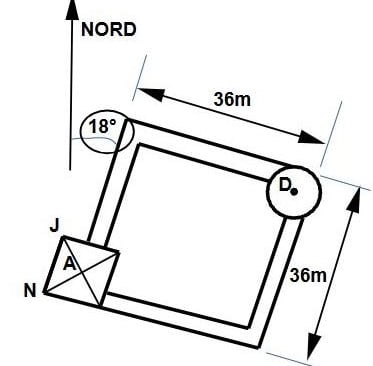
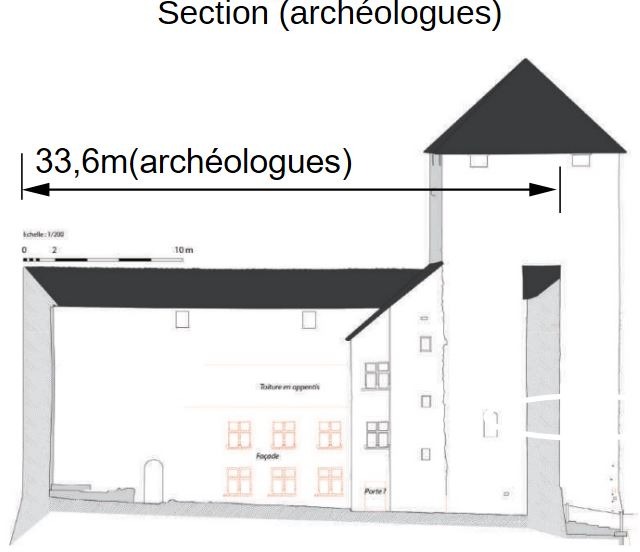
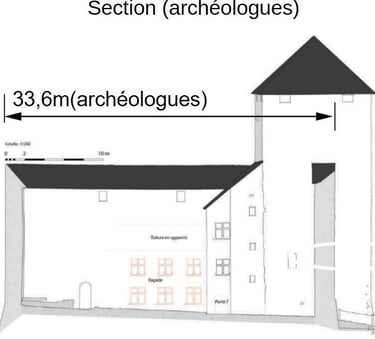
Nous allons essayer de vérifier la valeur de ce carré.....si carré il y a .... En étudiant, la configuration des lieux, on s'aperçoit qu'on ne peut pas mesurer directement le côté de la tour carrée extérieur. Mais on peut mesurer par la cour intérieur, et l'on peut aussi mesurer l'épaisseur des courtines. C'est ce que nous avons fait à 5 et voici les résultats finaux de ce que nous avons mesuré:

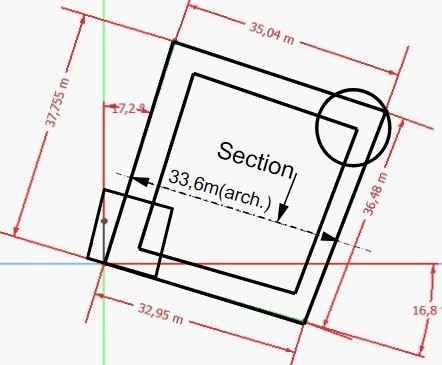
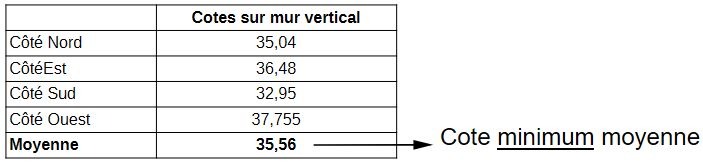
Les cotes sont prises extérieures, contre les parois verticales. On voit directement ici que cette enceinte principale n'est pas du tout carrée. Le cotes varient de 32,95m à 37,755m. Un écart absolu maximum de près de 4,805m.

Faisons la moyenne de ces cotes:

Les cotes sont prises extérieures, contre les parois verticales. Or, nous savons que des glacis sont présents aux bases des murs. Si bien qu'en fait, sur le seuil de la tour carrée, nous sommes ceinturés des glacis pour des raisons de défense. On peut donc dire que nous sommes sur une cote moyenne minimum de 35,56m.

Les archéologues ont effectués des relevés photogrammétriques, et l'on peut dans un premier temps vérifier si nos mesures son correctes.

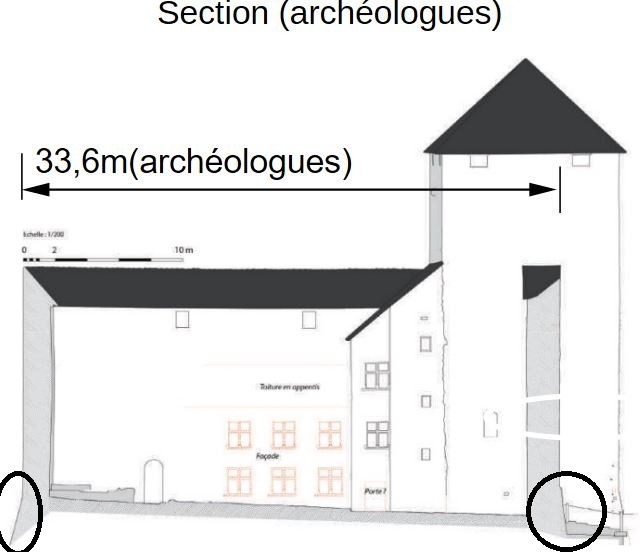
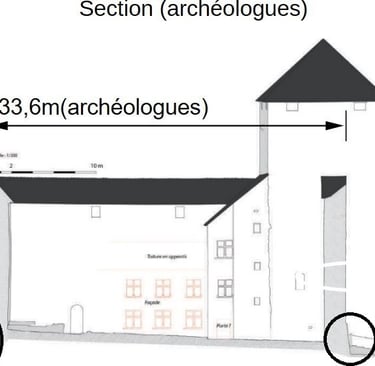
Or, nous pouvons voir que les glacis étendent la surface au sol. Sur cette vue, j'évalue à 25cm de chaque côté environ (e1 et e2).

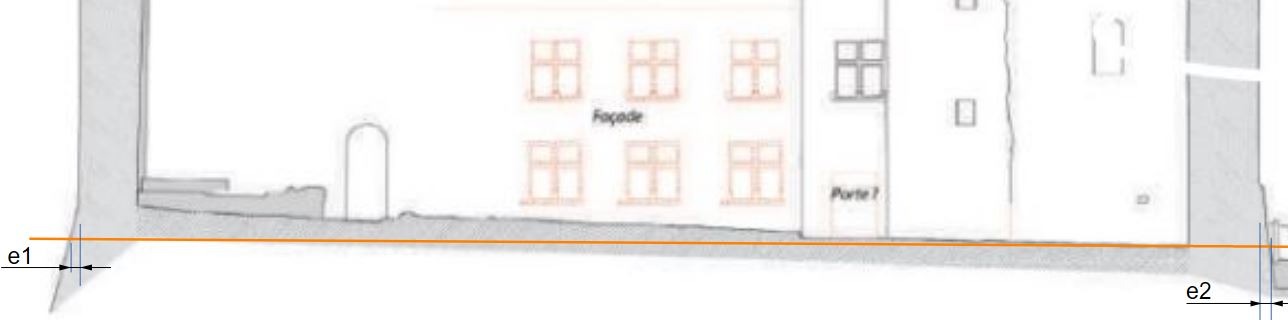
En mécanique, c'est ce que l'on fait lorsqu'on a des parties coniques, ou biseautées. On part d'une référence transverse au cône pour définir la position axiale des éléments. Ceci est appelé le plan de jauge (trait en orange pris au seuil de la tour carrée, par exemple). Et là on va pouvoir positionner verticalement ET les fondations, ET les éléments au dessus du sol.

Conclusion, la cote de 35,56m est une cote moyenne minimum entre mur, qui ne tient pas compte de l'envergure au seuil. Il faut rajouter entre 40 et 60cm. Ceci nous amène à une cote moyenne de 36 mètres environ.

Selon les archéologues, les constructeurs ont eu du mal à implanter les murs sur le socle rocheux qui constitue le château. Et en effet, on voit bien sur le site que cela devait être compliqué avec la roche à l'entrée du château.

Partir sur une intention d'un carré de 36m moyen est possible comme hypothèse, qui reste à confirmer par l'étude globale de l'architecture.

En effectuant une mesure Google Earth de l'orientation moyenne des murs, nous avons par ailleurs environ 18° moyen d'orientation de ce pseudo carré de 36m moyen. Ceci est une indication à prendre en compte.

Voici les glacis entourés:

Bibliographie:

¹. A. Kersuzan, "La mesure standardisée des toises de construction dans les châteaux forts du comté de Savoie, fin XIIIe siècle et XIVe siècle", Cahiers de métrologie tome 24-25, 2006-2007

². A. Kersuzan, Défendre la Bresse et le Bugey, pages 187 et 212, 2005.

³. Thérèse Sclafert, "Le Haut-Dauphiné au Moyen-âge", p 749, 1926

⁴. Nathalie Nicolas, "La guerre et les fortifications du Haut-Dauphiné", p 163 ,2005

⁵. Extrait des registres des arrêtés du Préfet du département de l'Isère, du 24 vendémiaire an 10.

⁶. Nicolas Payraud. Châteaux, espace et société en Dauphiné et en Savoie du milieu du XIIIe siècle à la fin du XVe siècle. Histoire. Université Lumière - Lyon II, p. 325, 2009.

⁷. Tables de comparaison entre les mesures anciennes du département des Hautes-Alpes et celles qui les remplacent dans le système métrique, publiées par ordre du préfet, p. 27.

⁸. Maria Muccillo, "Leonardo Fibonacci", treccani.it, 1997

⁹ . Des bâties de bois aux bâties de pierre - Laurent d'Agostino - Rediffusion Bastida, https://www.youtube.com/watch?v=JtJq-AbOj3U, 26'26''