Introduction au nombre d'or d'Ambérieu-en-Bugey à travers les châteaux médiévaux
le 5 janvier 2025
Nous avons vaguement évoqué la possibilité d'une relation au nombre d'or. Dans cette partie nous allons lier la cartographie à la métrologie pour montrer l'utilisation du nombre d'or dans l'unité du mètre pour organiser l'espace des châteaux médiévaux à Ambérieu-en-Bugey.
Pour rappel
Le nombre d'or est aussi appelé divine proportion. Toute chose formée à tendance à converger vers ce nombre en proportion (nature, architecture, etc...)
quelques propriétés du nombre d'or:
1,618²=2,618
1/1,618=0,618
1. Liens entre la cartographie et métrologie
Nous avons vu que les châteaux, par leurs nombres en distances, azimuts et altitudes , représentent une cartographie à l'échelle 1:1 de l'espace. Il a, de plus, été démontré en métrologie que le mètre a été employé pour définir les points caractéristiques de l'implantation du château des Allymes.
Revenons au bout de la colline de Saint-Denis-en-Bugey. refaisons le point de ce qui a été observé:
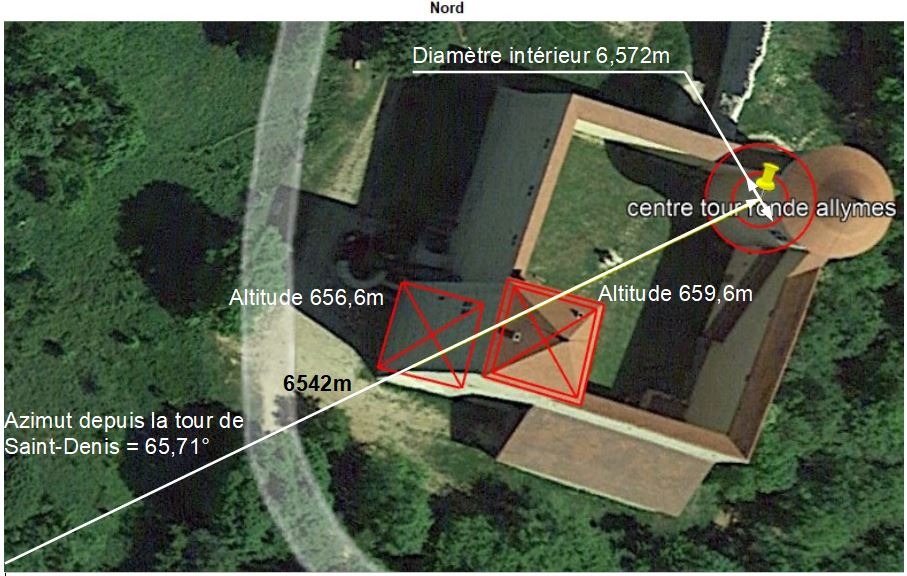
Le nombre 65 est redondant avons nous déjà dit.
Un nombre doit interpeller maintenant, c'est l'azimut de 65,7°. En effet, au Moyen-âge, le cercle ne se décompose pas en 360° décimaux, mais en degrés (°), minutes( ' ), et secondes ( '' ).
En effet, cercle se décompose aussi en 360°. Mais la partie non entière, la partie décimale est exprimée dans une base soixante au lieu de la base décimale.
Donc 1°=60' et 1 minute=60''
Ce système est dit sexadécimal (de base 60)
Convertissez l'azimut de 65,7°N en degrés (°), minutes( ' ), et secondes ( '' ). Puis observez le point de vue depuis la tour de Saint-Denis ci-dessous.
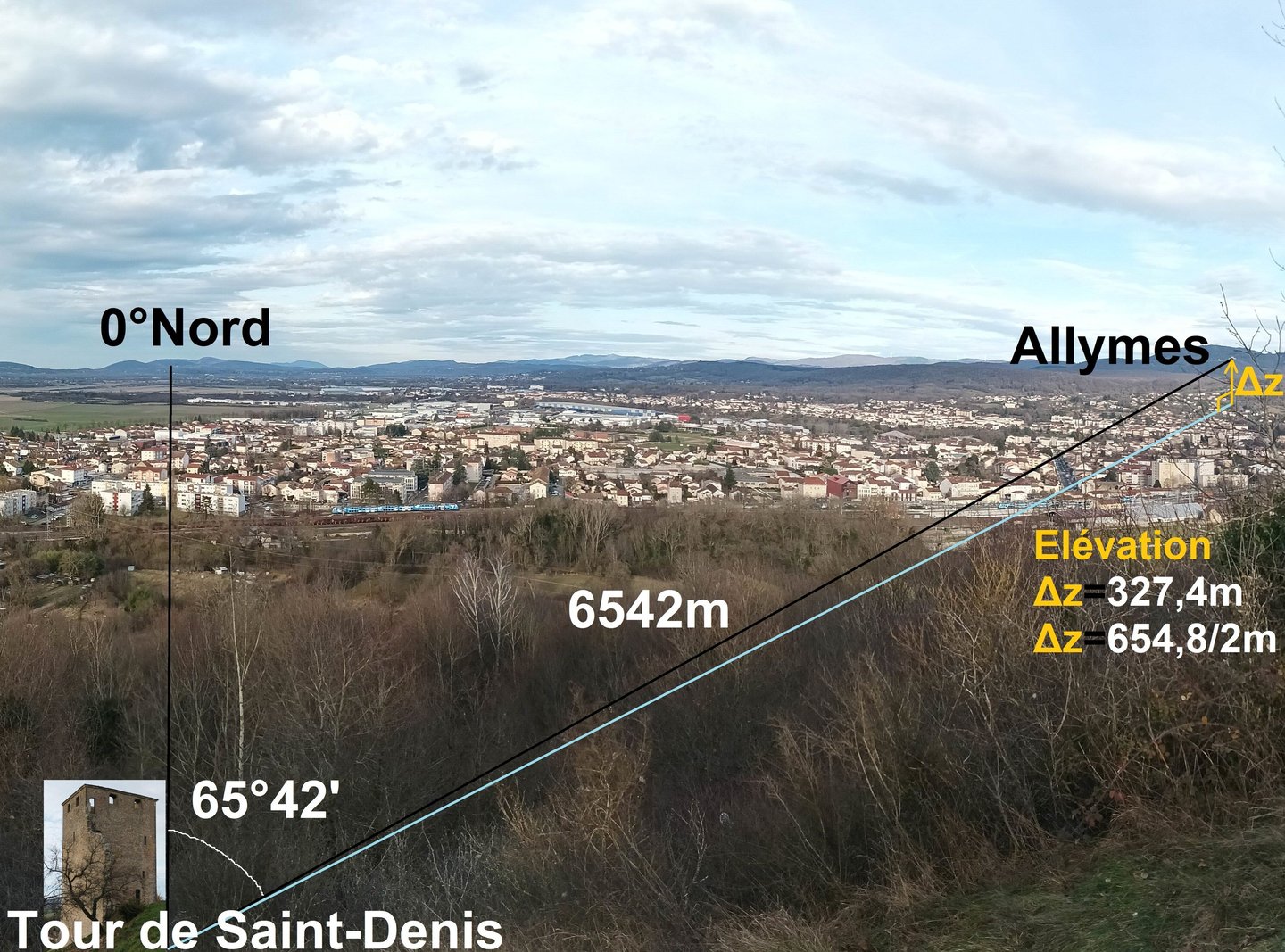
VOILA UNE DECOUVERTE MAJEURE DE L'ESPACE Ambarrois.
A la tour de Saint-Denis en Bugey, du XIVe s., je fais un angle de 65°42'Nord et j'observe le chateau des Allymes dont la tour Ronde est située à 6542m tout en coupant la cour du château dans la diagonale. Entre les 2 châteaux, le dénivelé positif est de 327,4m c'est à dire exactement 654,8/2 mètres.
Cela vient confirmer que l'espace a été cartographié. Et cela confirme l'utilisation du mètre au moins au XIVe s.. En effet, le hasard est ici nul puisque 6542 est un nombre qui revient sur deux unités dont les bases de calcul sont complètement différentes.
Mais alors, et le nombre d'or?
Je vous laisse essayer de le deviner un instant.
2. Le nombre d'or et 6542 à Ambérieu-en-Bugey
Le nombre d'or connait de multiples émanations. Trouver 618 ou 6,18 ou 161,8 ou 26,18 revient souvent au même, à cause du lien qui les unit, par l'élévation au carré, ou par l'inverse du nombre.
Mathématiquement, il est solution de l'équation du second degré:
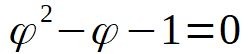
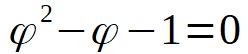
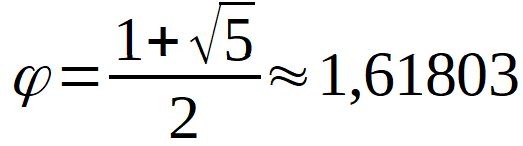
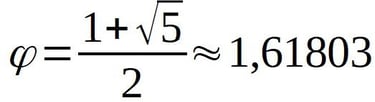
Il faut donc trouver le rapport qu'entretien 6542 au nombre d'or pour se faire une idée du lien qui les unit.
Je propose donc ces trois rapports:
6542/1,618=????
6542/0.618=????
6542/2,618=????
Conclusions ?
6542 est un multiple presque parfait de 2,618 par 5/2
6542 est quasiment le carré du nombre d'or divisé par deux. Donc (80,9)² =(161,8/2)² =6545
Et ceci est vrai à 99,98%
Mais alors, d'où vient l'erreur, et pourquoi l'erreur? cela s'explique-t-il?
ET d'abord, c'est quoi 6542?
Nous aurons l'occasion de voir l'explication dans un article ultérieur intitulé Cartographie 2.
3. Conclusion
Les raisons qui font que 6542 est le nombre d'or d'Ambérieu-en-Bugey sont:
qu'il est l'émanation du carré du nombre d'or;
qu'il organise l'espace en élévation, azimut, distances entre les deux châteaux;
que sont utilisation se traduit par des rejetons partout où il est possible de le faire.
Ce nombre d'or s'écrit dans le système métrique. Donc c'est le mètre qui est utilisé.
L'azimut vient confirmer que le nombre 6542 est fondamental, et ceci dans base autre que la base décimale. Donc 6542m est bien en mètres, et pas dans une autre unité. Je dis donc que le mètre date, au moins, du XIVe s et qu'il peut tout à fait avoir eu cours bien avant car nous sommes sur des point hauts censés être naturels.
