La cartographie d'Ambérieu en Bugey à l'échelle terrestre
Le 10 janvier 2025
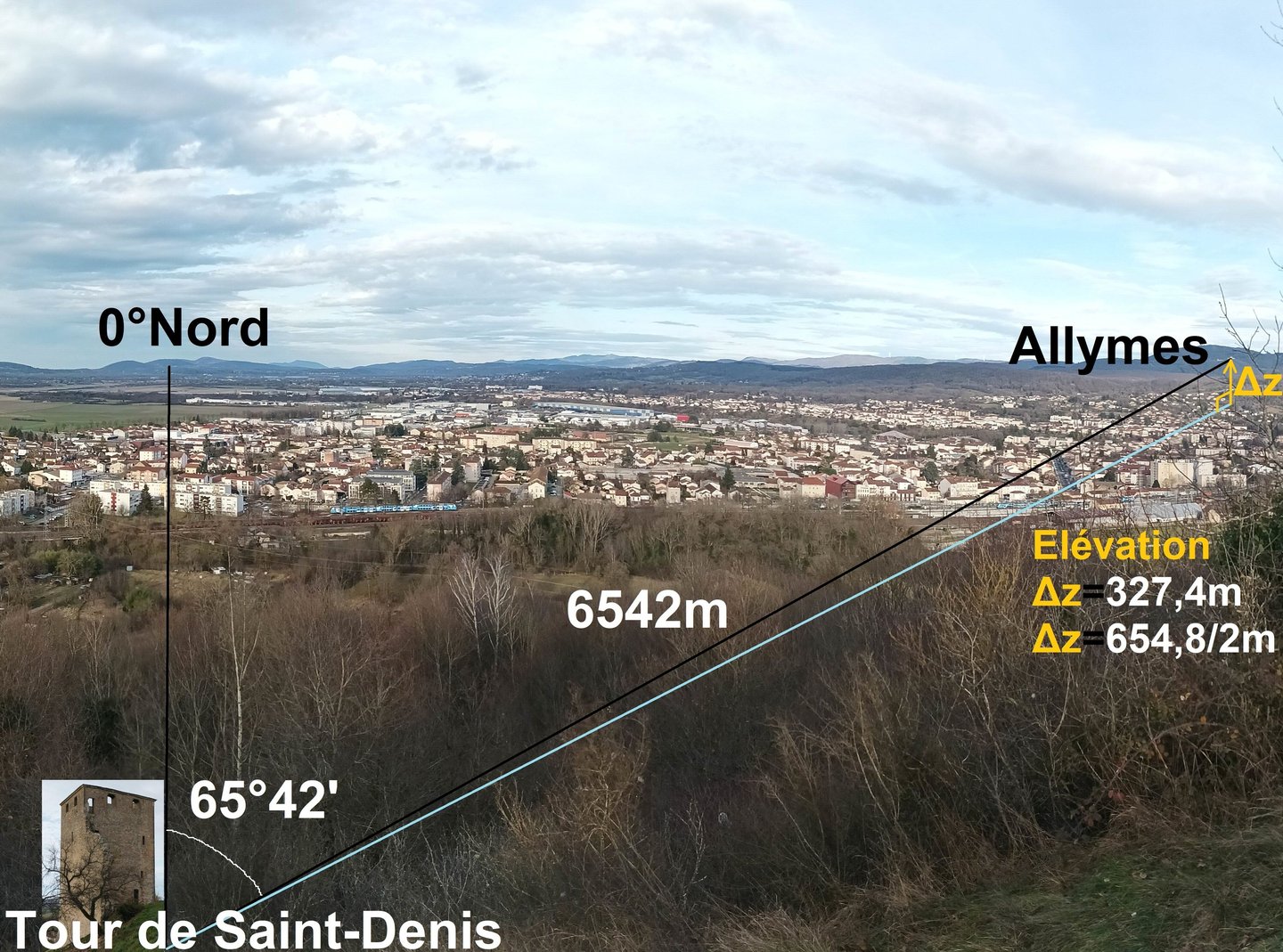
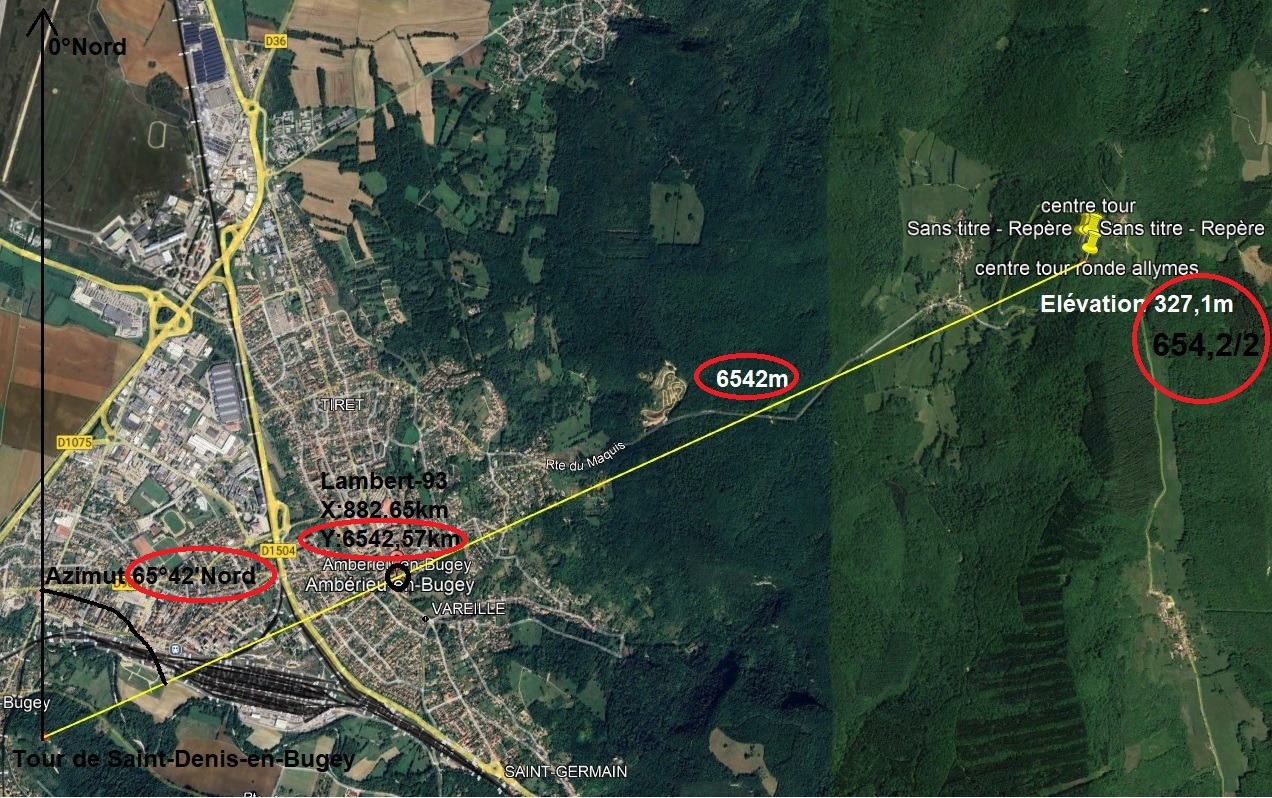
Et voici la configuration surprenante d'Ambérieu-en-Bugey à travers l'orientation du château des Allymes par rapport à la tour de Saint-Denis en Bugey. Cette figure est le pivot de notre démonstration, éloquente en terme de nombres et justifiant directement sans doute possible l'utilisation du mètre, au plus tôt au XIVe siècle (mais cela a pu être fait bien avant avons nous dit).
Mais finalement ne pourrait-on pas dire que ceci est du hasard? Les détracteurs les plus avisés ne manqueront pas de faire cette remarque.
Mais quelle est la probabilité d'avoir eu cette combinaison de nombres par hasard?
Comment retrouver 6540 sur 3 digits? Comment retrouver 65°40' sur 6×360 combinaisons? Comment tomber sur 327 quand on a 500 possibilités?
Et surtout que veut dire 6542?
C'est le lièvre que nous allons lever dans cette partie.
1. La question du hasard
D'abord, posons nous la question de la précision. Dans le cas le plus défavorable, je constate ±2 sur le 4ème digit (4ème chiffre significatif), et ceci est un grand maximum. Quiconque mesurera de centre de tour (au sol) à centre de tour (au sol) pourra le vérifier. Gardons donc les 3 premiers chiffres significatifs pour chaque nombre, puisque l'on a un intervalle de 6540 à 6544.
Deuxièmement, restons sur 3 digits. Donc imaginons un dé à 1000 faces. La probabilité de tomber sur LA bonne face 654 est de 1 pour 1000.
Pour la distance de 6542m, cela donne 6540m. Nous pouvons aller, sur 3 digits de 000 à 999, et ça fait 1000 combinaisons. La probabilité P(A) d'avoir le nombre 654 qui apparaît sur ce dé est de 1 pour mille. Pas facile à obtenir, mais possible.
Pour l'azimut de 65°42', cela donne 65°40' sachant qu'on ira de 10' en 10' d'azimut en prenant l'intervalle de tolérance cité précédemment. Donc le cercle possède 360°, et chaque degré peut être décomposé en 6 dizaines de minutes d'angle. Donc 6×360=2160 combinaisons. La probabilité P(B) d'avoir le nombre 65°40' qui apparaît sur ce dé est de 1 pour 2160. Pas facile à obtenir, mais possible.
Enfin l'élévation est de 327,4. Sur 3 digits, cela fait 327, moitié de 654. Cependant nous n'avons que 500 combinaisons cette fois-ci. En effet, 327, c'est bien 654, mais divisé par 2. La probabilité P(C) d'avoir le nombre 327 sur une base de 500 qui apparaît sur ce dé est de 1 pour 500. Pas facile à obtenir, mais possible.
Calculons la probabilité que les 3 évènements se produisent ensemble par hasard:
P(A) intersection P(B) intersection P(C)=(1/1000)×(1/2160)×(1/500)=1/1,08 milliards
C'est à dire que les 3 composantes cartographiques locales fondamentales nécessaires et suffisantes, (azimut, distance et élévation) entre les 2 monuments, présentent une probabilité d'avoir eu au hasard le nombre équivalent de 654 de 1 chance sur 1,08 milliards.
J'insiste. Ce sont les 3 composantes cartographiques locales nécessaires et suffisantes. Ce n'est pas la distance d'un lampadaire au château. J'ai pris centre de tour à centre de tour pour des châteaux qui sont contemporains, sur les 3 données cartographiques relatives locales uniquement.
Donc cela n'a pas été fait par hasard et au plus tard au XIVe siècle. Alors pourquoi 6542?
Les pistes de résolution sont mentionnées ci-dessus. Vous pouvez chercher avant d'accéder à la solution. Un indice: après la cartographie relative locale, pourquoi ne pas chercher dans la cartographie absolue, terrestre?
Cet article va expliquer la raison d'être de 6542. Car c'est bien de 6542 dont il s'agit, et non pas de 6540.
2. Différents types de projections cartographiques
Projection Mercator: nous la connaissons tous. La bonne vieille map monde. La France est au centre. L'Afrique est beaucoup trop petite mais la Russie et l'Alaska beaucoup trop grosses. En fait, on fait passer un cylindre autour de la terre pseudo-sphère et l'on projette chaque point sur le cylindre. Enfin, on déroule le cylindre et nous avons la carte de Mercator. Cette projection conserve les angles mais déforme les distances et les aires.
Maintenant faisons pareil avec un cône. En effet, le cylindre oblige à respecter la position à l'équateur. Mais ajustons un cône à l'endroit où l'on voudrait faire la carte exactement. On fera tangenter ce cône exactement à l'endroit choisi. Donc si l'on veut cartographier le France, Faisons un cône qui tangente en France! puis projetons les points sur ce cône, puis déroulons-le pour le mettre en plan. Nous obtenons une carte précise à l'endroit de la tangente. Les angles sont conservés mais il y a des altérations linéaires.
Il en existe d'autres mais nous allons les passer pour nous intéresser à la projection conique conforme de Lambert.
Beaucoup de projections existent, en fonction de la méthode, en fonction de la latitude, en fonction de si l'on veut garder les angles ou bien si l'on veut garder les distances.
Chaque pays utilise donc sa méthode de projection pour cartographier, au plus juste, et avec le moins de distorsions en angle ou bien en distances.
3. La projection conique conforme de Lambert
Johann Heinrich Lambert (1728-1777) est un mathématicien , philosophe et Astronome Mulhousien du XVIIIe siècle. Il présente notamment des travaux en cartographie conique conforme (qui conserve les angles) en 1772.
En France, les cartes IGN et la cartographie en générale sont basées sur la projection conique conforme de Lambert. La projection conique conforme de Lambert 93 (depuis un décret de 2000) couvre tout le territoire mais est un peu déformée. Aussi, est-elle est déclinée en 9 coniques conformes (2006): CC42, CC43, CC44, CC45, CC46, CC47, CC48, CC49, CC50. Elles permettent d'être précises sur l'ensemble du territoire qui va du 42ème parallèle environ au 50ème parallèle environ.
Il se trouve qu'elles viennent corriger la projection conique conforme de Lambert 93 qui couvre tout le territoire en passant par le 44ème et par le 49ème parallèle. Ce qui se trouve entre le 44ème et le 49ème est déformé sur la carte dans un sens, ce qui se trouve en dehors est déformé dans l'autre sens.
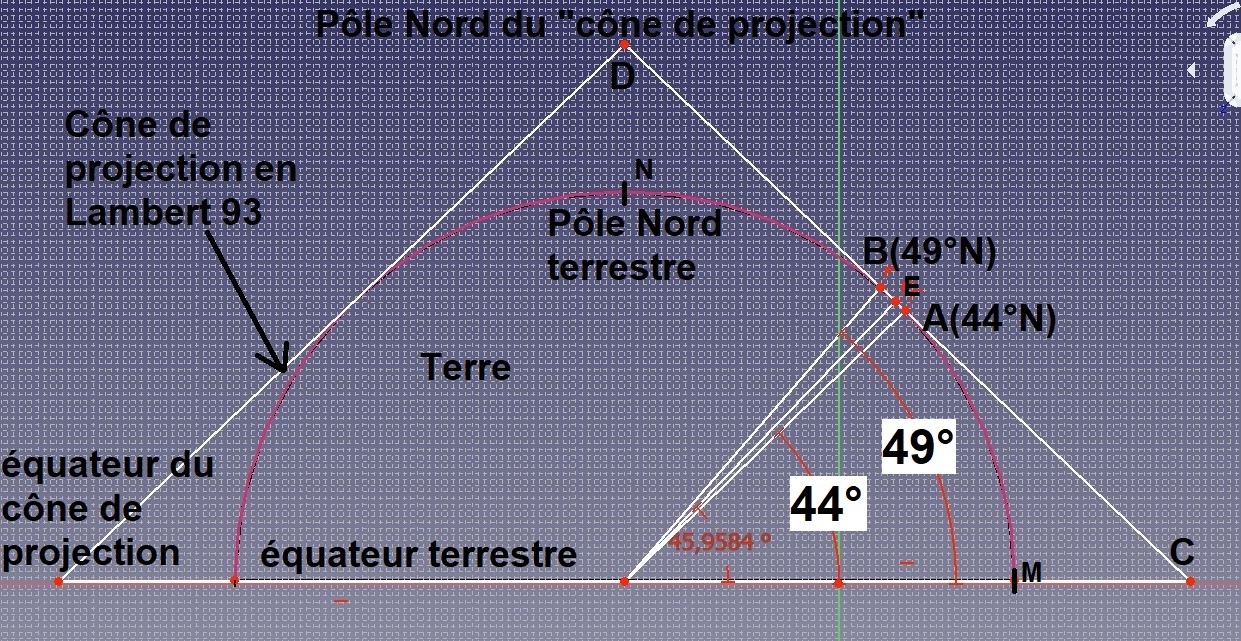
Pour le "Lambert 93" le cône passe par les 44e et 49e // en A et en B . On remarque que plus on va vers le pôle nord terrestre ou l'équateur, plus grande sera la déformation. Le Lambert 93 est donc une projection conique conforme qui est valable pour tous les pays qui se trouvent entre le 41e et le 51e //.
Méthode:
Tout ce qui se trouve sur l'arc MN de la pseudo sphère terrestre sera projeté sur la génératrice CD appartenant au cône. Il suffit alors de faire tourner légèrement le cône et de projeter chaque point de nouveau.
On voit que le plus l'on va vers C ou plus l'on va vers D, le plus la projection des éléments de la terre seront déformés. Le Lambert-93 est intéressant localement à l'échelle de la France.
Voici le développé d'une portion de cône en Lambert-93. Evidemment, tout ce qui est sur la même latitude que 44°N et 49°N est le moins déformé.
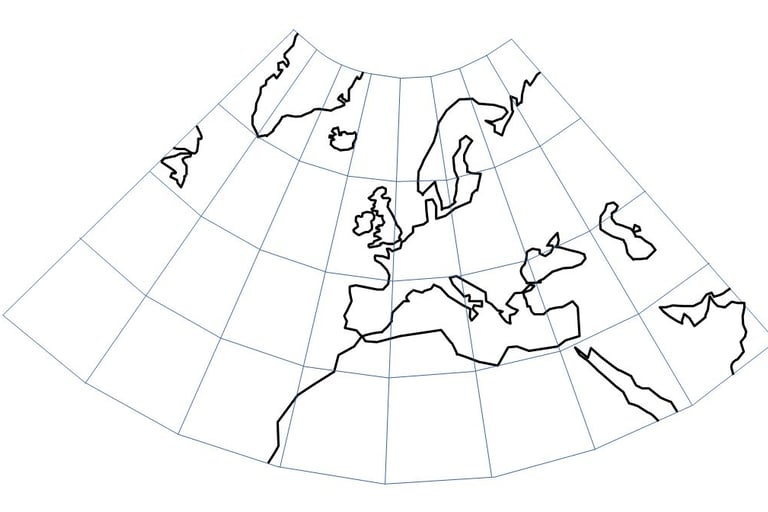
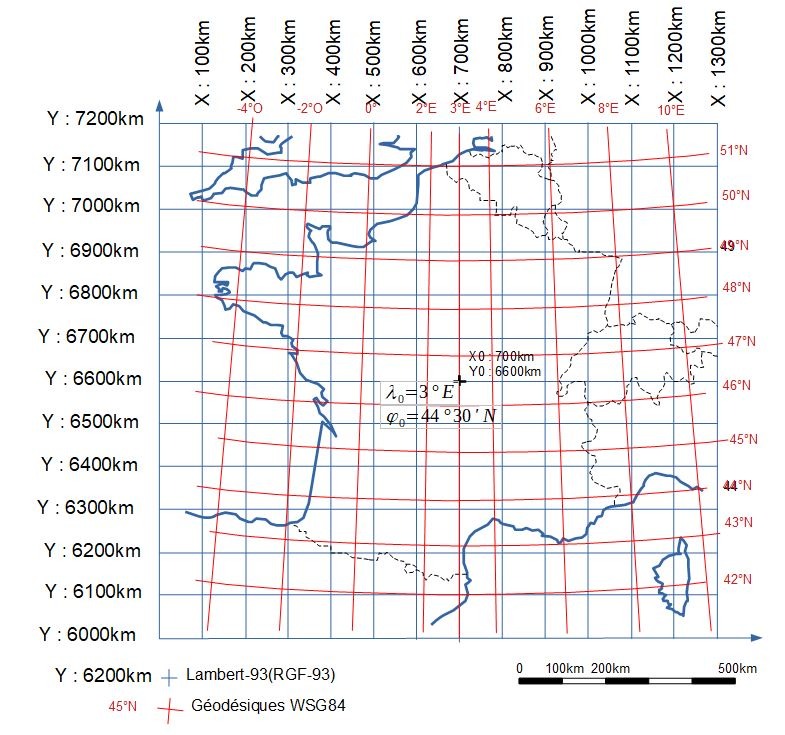
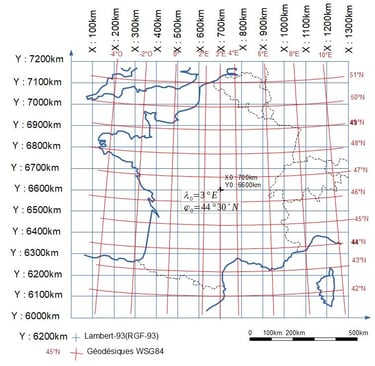
Le Lambert-93 étant particulièrement approprié pour cartographier la France , nous devons zoomer sur la partie la moins déformée et voici la France en Lambert-93
La coordonnée Y est la distance en km depuis l'équateur projetée sur le cône qui sera développé (par exemple la distance depuis le point C jusqu'à A). Pour X, l'origine est à 3°Est de Greenwich et considérée comme à 700 km du zéro. Donc l'origine est en X0:700km et Y0:6600km (Lambert-93) ou bien en coordonnées WGS-84 (lambda0=3°Est et phi0=46°30' Nord) et cela nous emmène en pleine campagne entre Moulins et Montluçon.
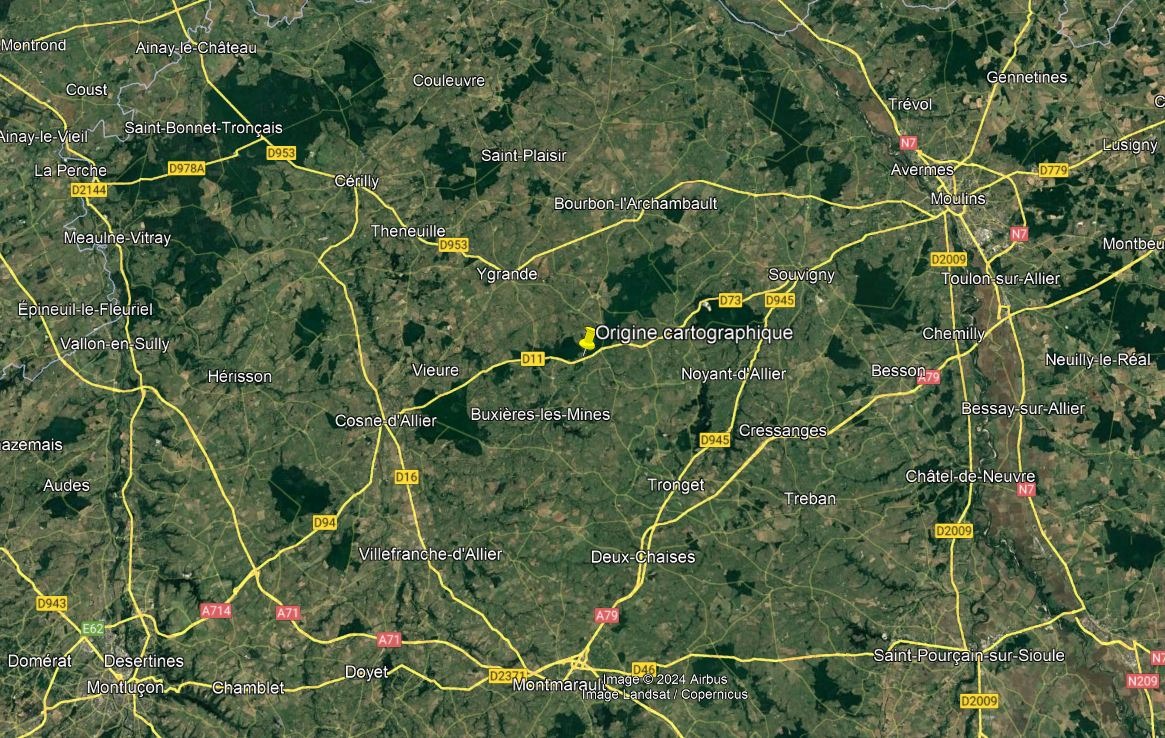
Rien d'incroyable à ce stade, et rien ne nous renseigne sur ce que l'on cherche. Nous devons revenir à Ambérieu-en-Bugey
4. Le "tiers-point" de 6542 d'Ambérieu-en-Bugey
Reprenons le Lambert 93. Nous avons vu que distance, azimuts et altitudes avaient une importance sur Ambérieu en Bugey.
Regardons voir les repères de nivellement d'Ambérieu-en-Bugey (géoportail)
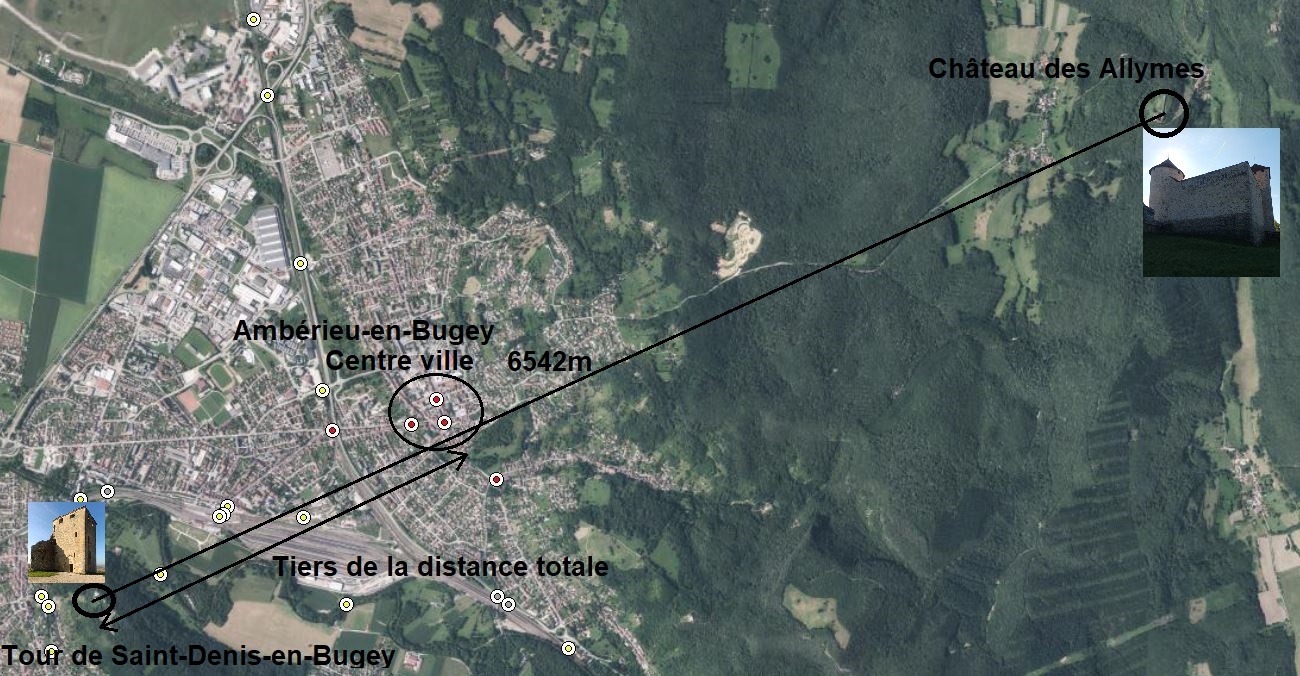
3 repères sont situés au centre ville. Nous avions déjà exprimé le fait, dans un autre article, que l'église est au tiers de la distance. Alors regardons au centre ville. Le repère de nivellement le plus proche de l'église et du tiers-point de la distance Saint-Denis/Allymes est le suivant:
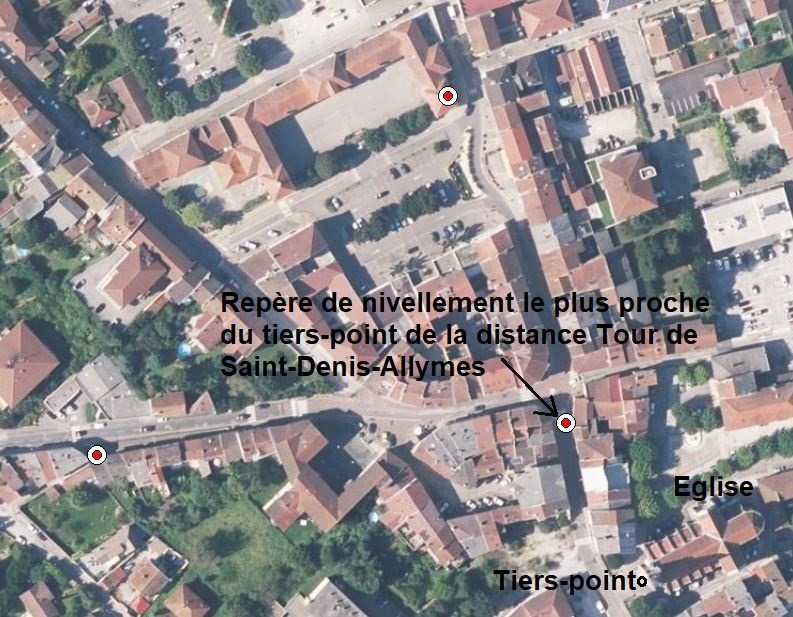
Voici le repère de nivellement qui indique 270m d'altitude. Il est situé à 74cm du sol (mesuré).
Dans géoportail, Chaque repère de nivellement possède une fiche repère de Nivellement associée. Je vous laisse aller voir sur:
https://geodesie.ign.fr/fiches/pdf/RP.AB-49_300564.pdf
Que peut-on remarquer?


Et voilà les informations les plus importantes données par géoportail à travers l'extrait de la fiche de l'IGN:


Nous voilà arrivés à une borne placée sur le chemin de la compréhension. Ces valeurs sont très précises.
Au tiers point de la distance de 6542m entre la tour de Saint-Denis et le château des Allymes, se trouve la coordonnée Nord en projection conique conforme de Lambert-93 exigée en 2000 par décret. Je n'ai pas de smiley pour décrire la situation...... mais explosion de rires quand même.
Au plus récent, donc, les gens du XIVe siècle ont remarqué qu'ils étaient à 6542,6 kilomètres de coordonnée Nord absolue en Lambert-93. Alors ils ont construit des châteaux sur le lieux important (peut être déjà matérialisé par autre chose) en réutilisant cette valeur cartographique absolue (6542,6) pour positionner et cartographier localement, en mètre et en ° ' ''.
MAIS C'EST IMPOSSIBLE
1799: mise en place du système métrique
1772: Lambert présente ses projections coniques conformes.
2000: un décret impose le Lambert-93 qui passe par les 44ème et 49èmeparallèle.
Par ailleurs, La France n'existe pas au XIVe siècle, et cela ne semble pas avoir de sens de prendre les parallèles du Lambert-93 pour faire du conique conforme.
Alors où est le problème? 700 ans avant d'avoir été imposé par un décret, le Lambert-93 est là dans les châteaux et au tiers-point exactement et en plus en mètres…
Cette information est inédite. Imaginez que les parallèles aient été choisis un peu différemment pour projeter en conique conforme. Par exemple prenons le 43ème parallèle et le 47ème parallèle. Cela aurait été judicieux aussi, puisque centrés sur le parallèle 45°N, qui est moitié de l'arc de sphère.
Et bien dans ce cas là, le 6542 km n'existe plus. D'ailleurs, c'est ce qu'il se passe quand on regarde les 9 coniques conformes locales ou d'autres projections de Lambert. La coordonnée nord changera automatiquement de nombre si l'on change les paramètres de sa projection.
C'est parce que les 2 parallèles sont centrés sur l'origine de 46°30' que cela marche.
Pourrait-on aussi dire que c'est au XXIe siècle que, ayant constaté la redondance des nombres à Ambérieu-en-Bugey, ils ont placé les parallèles 44 et 49 pile au bon endroit? je ne m'avancerais pas là-dessus. En effet, le Lambert-93 est projeté à partir du le RGF-93 (réseau géodésique Français). Le RGF-93 a en commun avec le WGS84 (utilisé par les GPS) l'ellipsoïde de référence IAG GRS80. Le Lambert-93 a été imposé pour tout un tas de raisons, notamment pour sa compatibilité entre les cartes utilisant les coordonnées Lambert 93 et les appareils GPS.
Ajouter à 3 données cartographiques locales basées sur 654, une donnée cartographique absolue basée sur 654, montre que la chance que cela se produise est de 1 pour 1000 milliards. Comme si l'on avait un dé à 1000 milliards de faces et que l'on tombe par hasard sur la bonne face …
Mais alors, on pourrait me dire "vous avez choisi la coordonnée Nord et pas la coordonnée Est, vous avez donc choisi la valeur qui vous arrangeait". Eh bien non, puisque la coordonnée Nord est la seule qui est absolue. En effet, on aurait pu faire tourner le cône sur la sphère autour de son axe et choisir n'importe quel point origine pour l'EST. Mais pas pour la coordonnée Nord car elle vient de l'équateur , base du cône en projection!.....ELLE SEULE EST UNE COORDONNEE PHYSIQUE ABSOLUE FONDAMENTALE. Et c'est d'ailleurs pourquoi elle est explicite en termes de nombres.
Mais remarquez, l'Est n'a pas été choisi par hasard non plus. Je vous propose de diviser la coordonnée EST par l'altitude locale (moins les 74cm pour être pile au niveau du sol, bien sûr)... alors? bluffant non?
Je dois donc finir par admettre que l'EST a aussi été choisi, et pas par hasard. Il a été quantifié.
5. Conclusion sur la latitude
Le mètre ne date pas du système métrique mais au plus tard au début du XIVe siècle, et massivement utilisé pour cartographier. Le mètre a donc pu être utilisé bien avant. Le mètre n'était par contre pas utilisé pour faire les comptes entre recettes et dépenses des châtellenies car nous n'en trouvons pas la trace. Les maîtres-artisans étaient payés à la Toise qu'ils avaient faite, ou au pied.
La projection conique conforme ne date pas de Johann Heinrich Lambert mais au plus tard au XIVe siècle.
La projection conique conforme Lambert-93 avait déjà été en place au XIVe ou très certainement bien avant. En effet, c'est parce qu'elle est centrée à l'origine en 46°30' par les parallèles 44°N et 49°N que la coordonnée nord d'Ambérieu est 6542,57. Sinon, cela ne marche plus. Par ailleurs, le Lambert-93 a été mis en place en 2000 pour de toutes autres raisons, et en particulier pour sa compatibilité carte avec les GPS.
Au plus tard au XIVe siècle ou même bien avant, on cartographie à l'échelle 1:1 localement, et de manière absolue sur le même site. Et c'est assez inédit et incroyable.
Nous avons répondu partiellement, mais dans une bonne mesure, à "pourquoi 6542?"
Des articles suivront pour s'intéresser à "Quand cela a-t-il pu être fait?".
Pour aider au développement n'hésitez pas à liker et partager sur les réseaux!
https://www.les-4-chemins.org/
Tik Tok : @château-du-bugey
6. Et pour la longitude?
Nous renvoyons le lecteur aux articles sur la métrologie. Nous avons vu dans ces articles comment les différentes "pièces" du château des Allymes ont pu être positionnées les unes par rapport aux autres.
En particulier, le positionnement de la petite tour ronde nord mérite que l'on s'arrête encore dessus. Elle est placée selon un plan modulaire carré de 5×11. 119m de longueur sur le côté 11, et 1190/22m sur le côté 5.
D'un point de vue numérique:
1190/22=54,09m±0,05
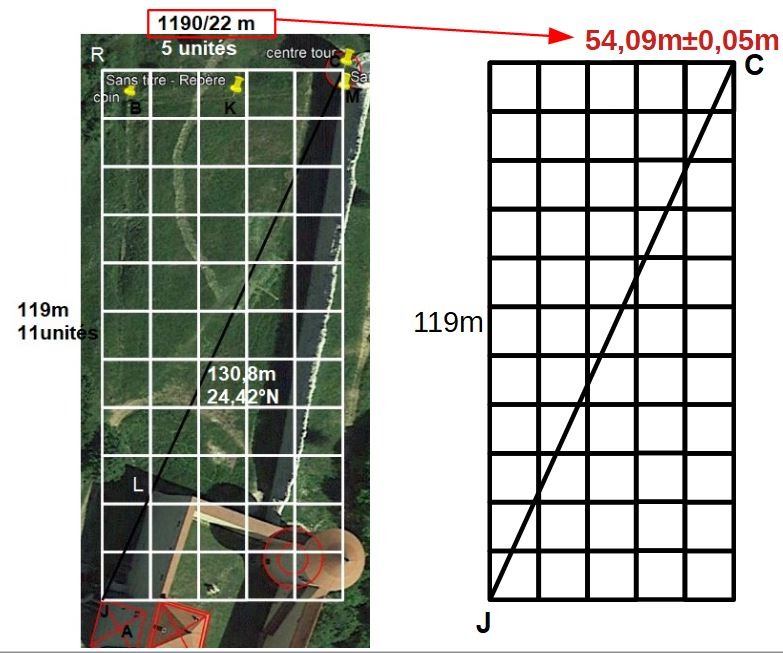
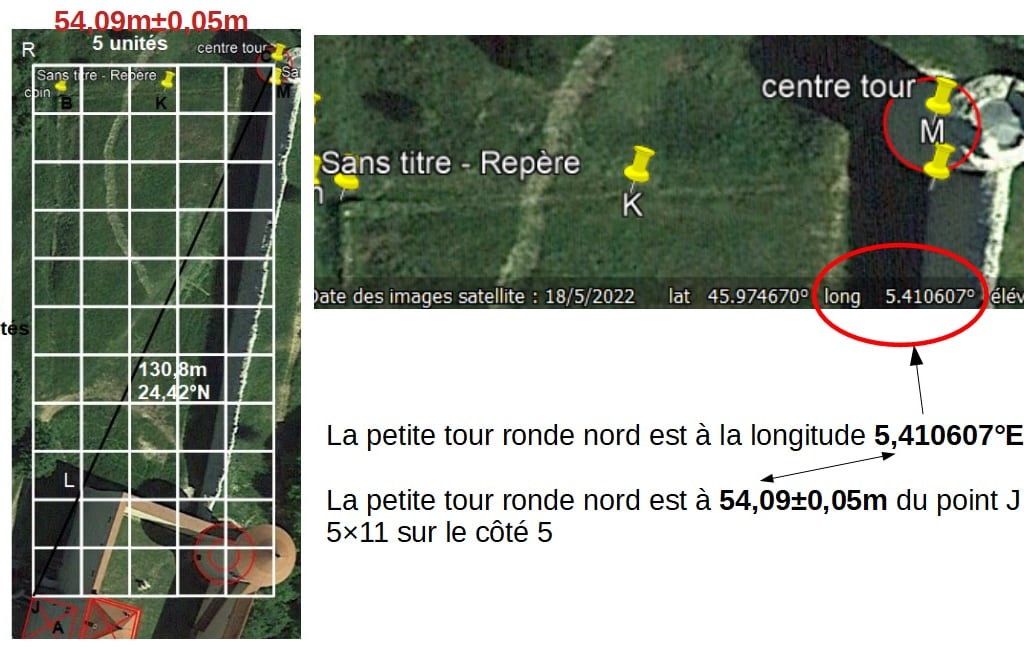
Or il se trouve qu'à cet endroit là, exactement, nous trouvons sur Google Earth Pro la valeur de la longitude en degré décimaux qui vaut 5,4106°EST.

Nous avons déjà vu la faible probabilité d'avoir le nombre 6542 intervenant dans le positionnement relatifs des châteaux, ainsi que sur la projection en Lambert 93.
Nous avons aussi vu que l'angle de la tour carrée au point J est le point de référence pour construire le mur OUEST vers le point B. Et le point B, nous avons vu qu'il est à 120m plein NORD du centre de la tour carrée (point A). Le point J est donc un point MAJEUR de la construction du château.
Ici, nous avons un plan modulaire carré très précis positionné justement par rapport au point J, et le point L est par ailleurs aligné avec la diagonale de ce plan modulaire carré, qui positionne le centre de la tour ronde au nord en C.
Enfin, le côté 5 fait 54,09m et la longitude de 5,4106°EST.
Géométrie, nombre, et cartographie sur les longitudes sont donc mises en œuvre, de nouveau.
7. La longitude et le temps
Les longitudes marquent l'écoulement du temps et sont marquées par 360 méridiens orientés Nord-SUD.
Un méridien de référence est situé à Londres, c'est le méridien de Greenwich. C'est l'heure "absolue" définie par l'homme suite aux travaux du royaume d'Angleterre aux XVIIe, XVIIIe et XIXe siècles.
Or, 360° pour le tour de la terre s'écoule en 24h.
Cela fait donc 15° pour une heure passée.
Si l'on prend un demi disque vertical découpé en 12× 15° à l'équinoxe, on mesure le temps dans la journée sans problème en fonction de la position du soleil.
Or le château des Allymes est à 5,41 degrés décimaux EST du méridien origine.
Cela donne 1298,4 secondes. Soit 21' 38''.
Est-il utile de rappeler la redondance du nombre 13 dans la géométrie des lieux?
La cour fait 1300m²
La distance JC fait 130,8m
La distance JL fait 26 m
Etc....
8. Conclusion sur la longitude et le temps
Le mètre n'est pas censé exister au XIVe siècle, or on trouve le même code numérique en degré décimal et en mètre. Le mètre a été utilisé;
Le degré décimal existe pour les même raisons , au XIVe siècle;
Le méridien de Greenwich a été placé au XVIIIe siècle. Il a même été repositionné en 1984 à 120m de décalage. Or nous sommes exactement sur la valeur numérique. Cela interroge sur le méridien de Greenwich....enfin sur une référence longitude qui est bien plus ancienne à Greenwich.
