L'étonnante configuration tour de Saint-Denis / château des Allymes (Ain). Les nombres et la géométrie.

1. Méthode

Pour étudier la géométrie des lieux à travers les nombres et unités de mesure, il faut des instruments de mesure. Parmi les outils numériques utilisables pour étudier la configuration entre le Château des Allymes et la tour de Saint-Denis-en-Bugey, nous avons notamment Google earth et géoportail. Ceci peut être fait à moindre coût. Le terrain nous apporte aussi des informations. Commençons par là.

Nous verrons par la suite comment les arts majeurs, avec le quadrivium, peuvent nous aider à mettre de l'ordre dans les observations de terrain.

Pour aller vite et passer les rébarbatifs paragraphes, le résultat de l'étude est:

Il existe des nombres caractéristiques sur leurs deux premiers chiffres significatifs sur l'axe Tour de Saint-Denis / château des Allymes. Ceci est vrai pour l'altitude, l'azimuth, la distance, et l'architecture sur place. Et cela commence par le 65.

2. Observations de terrain

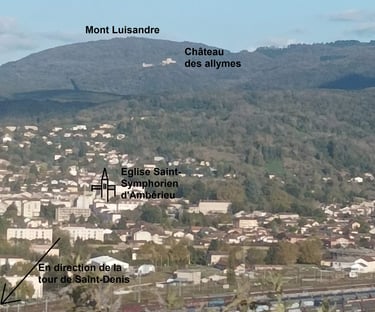
A la tour de Saint-Denis, Une vue presque à 360° s'offre à vous. Retournons nous vers le Château des Allymes. Voici ce que nous observons:

• Les courtines du château des allymes semblent nous faire face par l'angle et nous ne voyons pas la tour ronde derrière. Hypothèse 1 d'une diagonale de l'enceinte des Allymes tracée depuis la tour de Saint-Denis envisagée .

• Tour de Saint-Denis, château des Allymes et église presque alignés mais non alignés exactement. Hypothèse 2 de l'alignement à étudier

• L'église semble nous faire face exactement. Le transept semble perpendiculaire à la ligne de visée, pendant que la flèche nous fait face. Hypothèse 3 de l'alignement du faîtage dans cette direction exactement à valider (ou à réfuter).

• Le mont Luisandre, beaucoup plus haut n'est pas aligné avec tour de Saint-Denis et château des allymes.

Château des Allymes, vu depuis la Tour de Saint-Denis (Ain)

3. Etude de la distance entre les tours carrées des 2 châteaux, Saint-Denis et Allymes

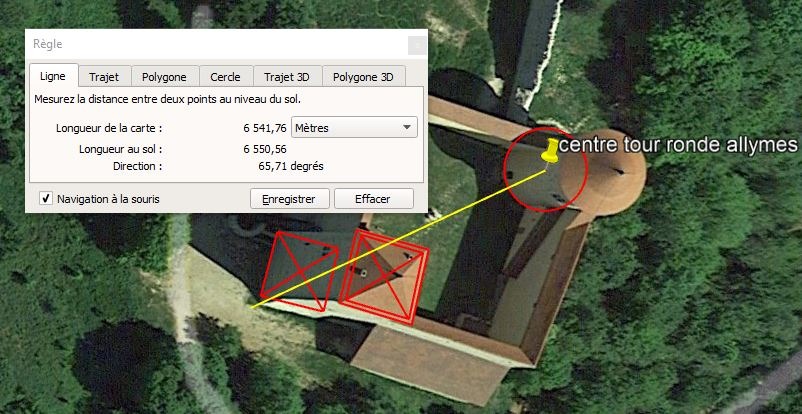
Prenons la distance entre le centre du pied de la tour de Saint-Denis et le centre du pied de la tour "presque carrée" du château des Allymes.

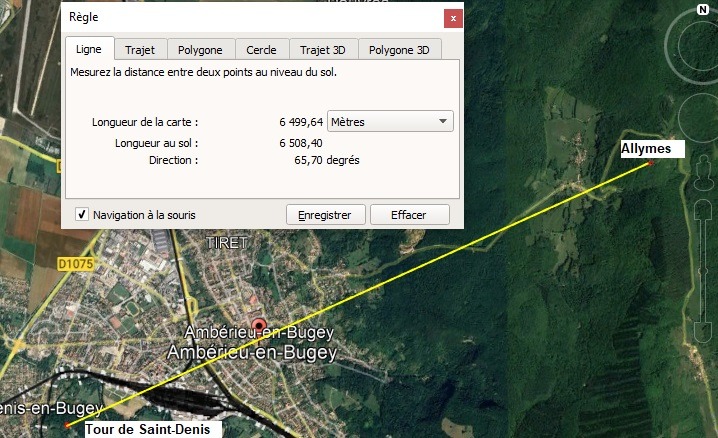
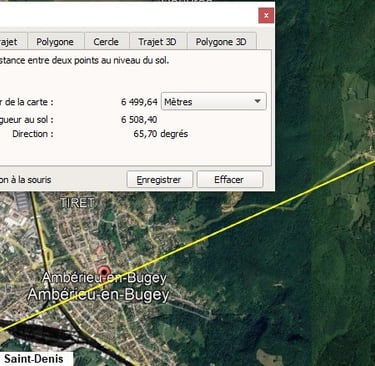
Distance entre tour de Saint-Denis et Château des Allymes, de tour à tour

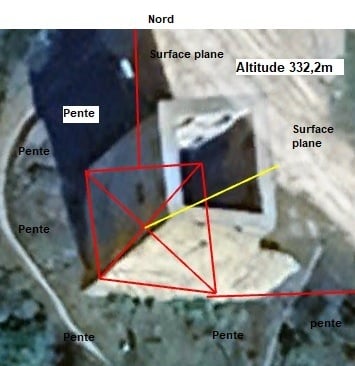
La longueur de la carte correspond à la distance entre les deux points directement, mais sur le plan de la carte de Google Earth pro.

La longueur au sol est la distance en ligne droite, au sol, et franchissant tous les dénivelés.

Nous prenons le centre des tours "presque carrées" sur la face au sol. Des erreurs de mesure avec leur implantation sur des dénivelés existent. Toutefois, en gardant cette prise de mesure "centre des tours au sol", les erreurs vont dans le même sens, et donc ne s'ajoutent pas.

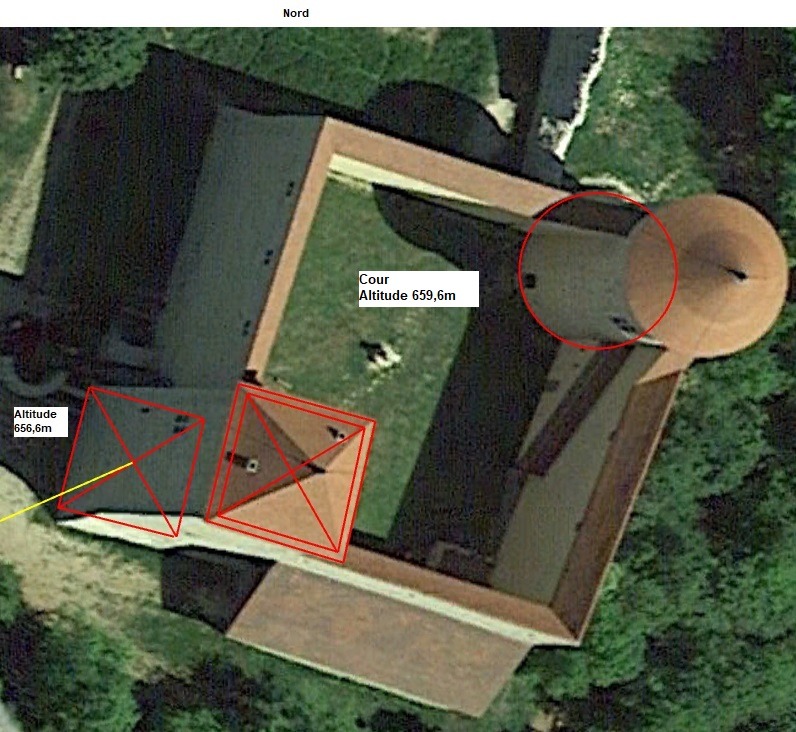
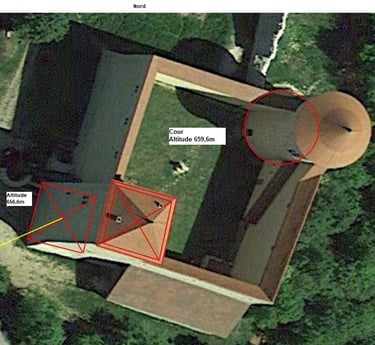
Allymes, centre de la tour et altitudes

Tour de Saint-denis, centre de la tour et altitudes

Mesures

• Longueur de la carte entre les 2 tours = 6500 ±1 mètres ;

• Azimut = 65,7° Nord;

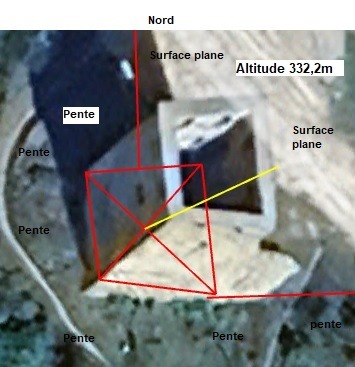
• Altitude de départ = 332,2m ; (géoportail)

• Altitude d'arrivée 1 =656,6m; (géoportail) à noter cependant que la terre a été relevée au XIXe siècle de 3m environ

• Altitude d'arrivée 2 = 659,6m; (géoportail)

Remarques

• Il semble que la combinaison 65 suivi d'un nombre revient plusieurs fois: sur une distance en mètre ou sur une direction (azimut) en degré ou encore sur une altitude en mètre;

• L'altitude d'arrivée est très proche du double de l'altitude de départ. en gros 330m × 2 = 660m.

Conclusion 1

Il semble qu'une suite de nombre se dégage avec une fréquence un peu curieuse selon l'ordre 65 suivi d'un nombre différent.

Deux cas de figure peuvent être envisagés:

• Les bâtisseurs médiévaux ont choisi les point hauts les plus stratégiques pour établir leur défense. Dans ce cas aucune configuration ou relation d'ensemble n'est possible puisque le terrain a, à lui seul, présidé au choix du lieu de défense.

• Les bâtisseurs médiévaux ont choisi les points hauts les plus stratégiques pour établir leur défense ET qui correspondent à une implantation d'ensemble ayant un sens qui va plus loin que le simple fait de faire la guerre.

Dans le premier cas, nous pouvons nous en arrêter là et attendre qu'historiens médiévistes et Archéologues puissent nous en apprendre plus. Et d'ailleurs, nous pouvons les suivre avec intérêt à ce sujet.

Dans le deuxième cas, appuyons nous sur les arts libéraux (quadrivium par exemple) pour essayer d'aller plus loin et de comprendre le cœur de la pensée ancienne (médiévale et antérieure).

4. Les arts libéraux médiévaux comme voie et comme but

En grèce antique, les 7 arts majeurs (Quadrivium et Trivium) étaient étudiés par les écoles de pensées de Pythagore, Platon, Aristote.

Le quadrivium est composé des nombres, de la géométrie, de l'astronomie et de la musique.

Le trivium est composé de la réthorique, de la dialectique et de la grammaire.

A la fin de l'Antiquité, On en retrouve trace chez Nicomaque de Gérase (vers 150 apr. J.C.) puis chez Boëce ( vers 500 apr. J.C.). Ce dernier écrit notamment son Institution arithmétique qui reprend largement Nicomaque de Gérase.

Le Moyen-âge voit l'utilisation des 7 arts majeurs (arts libéraux) se développer.

Ainsi, Humbert II de la Tour du Pin, dernier Dauphin de Viennois, était connu pour être un humaniste, religieux, développant une appétence particulière pour les arts libéraux¹.

Boëce, dans son Institution Arithmétique, laisse penser que "ces sciences sont à la fois une propédeutique et une partie de la philosophie" ². Donc, un chemin préparatoire à la philosophie, mais aussi une partie elle-même de la philosophie.

Regardons de plus près les nombres et la géométrie entre Saint-Denis et les Allymes.

5. Nombres, géométrie et curiosités entre la tour de Saint-Denis et le château des Allymes

Longueur de la carte entre tour de Saint-Denis et tour carrée du château des allymes

• Longueur de la carte entre les 2 tours = 6500 ±1 mètres ;

• Azimuth = 65,7° Nord;

• Altitude de départ = 332,2m ; (géoportail)

• Altitude d'arrivée pied de la tour =657±1m; (géoportail)

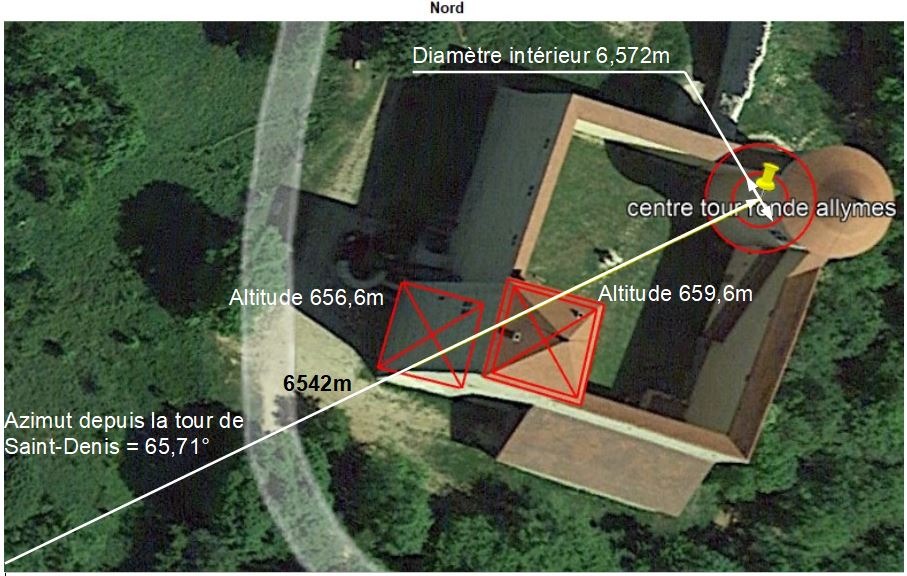
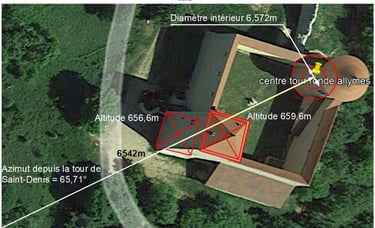
Longueur de la carte entre tour de Saint-Denis et tour ronde du château des allymes

• Longueur de la carte entre les 2 tours = 6542 ±1 mètres ;

• Azimuth = 65,71° Nord;

• Altitude de départ = 332,2m ; (géoportail)

• Altitude d'arrivée 2 = 659,6m; (géoportail)

Curiosités entre tour de Saint-Denis et tour carrée du château des allymes

• Azimut et altitude finale présentent une valeur numérique identique sur les 3 premiers chiffres significatifs. C'est remarquable.

• La distance tour à tour semble être de 6500m exactement. Reprenant les 2 premiers chiffres significatifs, la mesure semble exacte en mètre.

• Différence d'altitudes entre l'arrivée et le départ= 657-332=325. Or, 325 est le vingtième exactement de 6500.

Curiosités entre tour de Saint-Denis et tour ronde du château des allymes

• La distance est de 6542m. Soit 2 × 3271

• Différence d'altitudes entre l'arrivée et le départ= 659.6-332.2=327,4.

• Le nombre qui a la suite de 327 semble avoir une importance puisque répété 2 fois sur la distance.

Curiosité sur la géométrie

Ce château n'a pas de géométrie parfaite. La tour n'est pas carrée exactement, les courtines ne forment pas un quadrangle carré exact, etc.

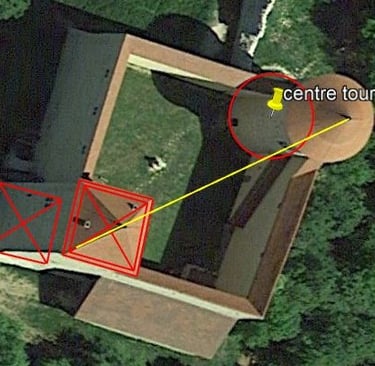
Cependant, depuis la tour de Saint Denis qui est située bien loin, la distance passe par les centres des deux tours du château des Allymes exactement.

On peut le voir précisément en prenant les pointes des 2 toits.

L'HYPOTHESE 1 EST VERIFIEE

Curiosités sur les nombres

327

comme 1/20ème de

6540

657

et

325 comme 1/20ème de 6500

Nous pouvons représenter graphiquement l'utilisation du nombre 327 de la manière suivante, sous forme géométrique de 20 carrés de côté 327 exactement

Sous des allures de nombres qui tournent autour de 65 suivi d'un autre nombre qui semble aléatoire, nous nous apercevons d'une importante précision.

Voici les mesures entre la tour de Saint-Denis et la tour ronde du château des Allymes:

On va plus loin?

Le diamètre intérieur de la tour cylindrique, sur un enduit certes récent, mais dont l'épaisseur n'est pas significative, mesure......

6,572 m ± 4mm

6. Le quadrivium: les nombres

Nous constatons qu'aucune notion de mathématiques n'est utile jusqu'à présent. Il ne s'agit que d'observations.

Faisons un tout petit peu de mathématiques selon deux manières différentes

NOTATION MODERNE

6500 = 6 × 10³ + 5 × 10²

6 est le chiffre des milliers et 5 est le chiffre des centaines.

Les nombres sont des quantités à acquérir. La quantité a une importance pour celui qui l'utilise. Pensons au salaire que l'on touche par exemple. Ou bien aux prix.

NOTATION A LA MANIERE DU QUADRIVIUM

6500 = 5 × 13 × 100

5 et 13 sont les nombres premiers qui composent le nombre 65.

Les nombres ont ici une qualité.

Que ce soit altitudes, ou distances, ou azimuts, le 6 suivi du 5 ont une importance. On peut remonter aux nombres premiers pour essayer de comprendre quel nombre important est sous-entendu.

100 ne représente qu'un changement d'échelle de base 10. 100 joue uniquement sur la quantité. Pas sur la qualité.

Autre exemple quadrivium

327 = 3 × ...?..

Le nombre manquant va nous intéresser particulièrement.

7. Le quadrivium: la géométrie

Retour sur les hypothèses formulées depuis le terrain.

Hypothèse 2: l'église est-elle alignée avec le château des allymes et la tour de Saint-Denis.

Nous voyons sur l'image que l'église est décalée par rapport à l'axe tour de Saint-Denis / château des Allymes. Le décalage est faible par contre: 23 mètres.

Hypothèse 3: Le faîtage de l'église possède-t-il la même direction que l'axe tour de Saint-Denis / château des Allymes?

Nous voyons sur l'image que le faîtage de l'église ne possède pas la même direction par rapport à l'axe tour de Saint-Denis / château des Allymes. Le décalage angulaire est très faible par contre: 2,1 degrés.

Nous avons déjà vu pour le Château des Allymes que, malgré les formes non parfaites des "carrés", il existe quelque chose qui dépasse ce premier point de vue.

De plus, l'église ancienne n'était peut-être pas exactement à cet emplacement (voir la section sur les monuments).

Nouvelle hypothèse pour l'église: se pourrait-il que pour l'église, malgré les imperfections d'alignements, il existe un code numérique à la manière de l'axe Saint-Denis/Allymes?

8. Les nombres et la géométrie pour l'église Saint-Symphorien d'Ambérieu sur l'axe tour de Saint-Denis / Allymes

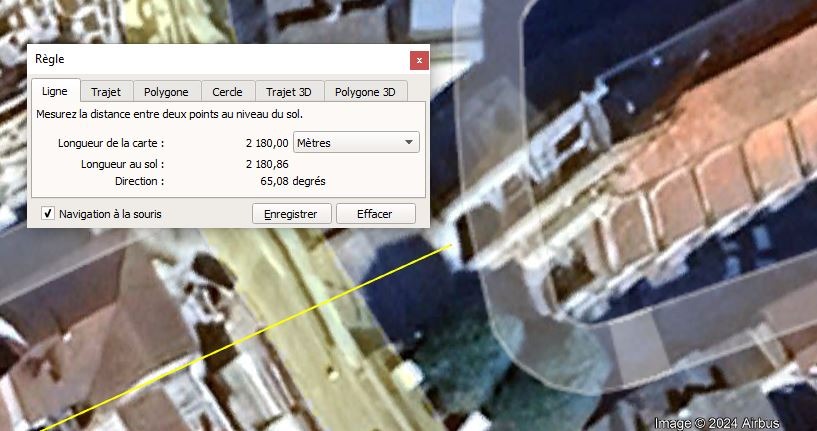
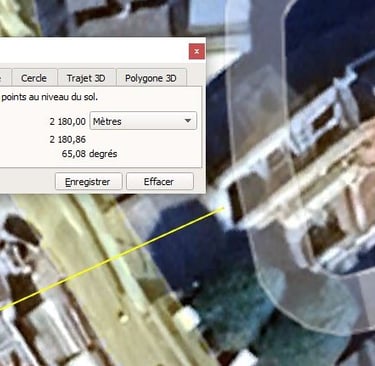
Et voici la longueur de la carte entre tour de Saint-Denis et entrée de l'église.

Longueur de la carte entre tour de Saint-Denis et l'église

• Longueur de la carte entre les 2 bâtiments = 2180 ±1 mètres ;

• Azimut = 65,08° Nord;

• Altitude de départ = 332,2m ; (géoportail)

• Altitude d'arrivée pied de la tour =272±0,5m; (géoportail)

Remarquable

• 2180=2×109×10 et nous retrouvons bien le 109 (= 327/3);

• 4×272=1088 et nous retrouvons donc le 109.

9. Récapitulons uniquement avec le nombre 109

• La différence d'altitudes tour Saint-Denis / Tour ronde des Allymes = 3 × 109

• La distance tour Saint-Denis / Tour ronde des Allymes = 60 × 109

• L'altitude de l'église d'Ambérieu = 109 × 10 / 4

• La distance tour Saint-Denis / église d'Ambérieu = 109 ×20

• Par voie de conséquence, la distance église d'Ambérieu / Tour ronde des Allymes = 40×109

10. Changeons d'unité

Pied anglais à 30,48 cm

• La différence d'altitudes tour Saint-Denis / Tour ronde des Allymes = 3 × 358.049

• La distance tour Saint-Denis / Tour ronde des Allymes = 60 × 357.72

• L'altitude de l'église d'Ambérieu = 356.955 × 10 / 4

• La distance tour Saint-Denis / église d'Ambérieu = 357,612 ×20

• Par voie de conséquence, la distance église d'Ambérieu / Tour ronde des Allymes = 40×357,776

Nous voyons ici que la valeur du module tourne autour de 357,622 pieds anglais.

Cependant, les coefficients multiplicateurs restent les mêmes.

Donc dans n'importe quelle unité, nous verrions apparaitre toujours un nombre qui reviendra, avec ses multiples associés en nombre entier.

La particularité du 109, en mètres donc, c'est que c'est un nombre premier (et donc entier).

Conclusion

Ce qu'il faut retenir de cette page, c'est qu'une fréquence élevée d'un nombre ou de l'un de ses multiples, dans une unité de mesure, pour mesurer une distance, ou une altitude, ou un azimut est un indicateur certain. Cela est vrai pour de longues distances (tour à tour), et cela va jusqu'au diamètre intérieur de la tour.

Et le remarquer ouvre des perspectives.

Retenons aussi le nombre 109, comme nombre premier (divisible uniquement par 1 et lui-même).

Retenons enfin que l'on semble constamment partir du nombre, puisqu'utilisé simultanément sur l'altitude et sur les distances. Utilisé aussi sur un azimut en degré. Et pour finir, utilisé dans la construction humaine d'une tour ronde.

Bibliographie

¹ P.Fournier, le Dauphin Humbert II, Académie des inscriptions et belles-lettres, bulletin de novembre 1912, p.582

² Jean-Yves Guillaumin. Le statut des mathématiques chez Boèce. In: Revue des Études Anciennes. Tome 92, 1990, n°1-2. pp. 121-126;