L'astronomie peut-elle se retrouver inscrite dans le "tissu" des châteaux?
Le nombre structure l'univers. Cette citation reprise d'un certain nombre de pythagoriciens ou de commentateurs de Pythagore, ou des platoniciens est à l'origine de la science des anciens.
Ainsi:
Le nombre qui se déploie dans l'espace terrestre, c'est la géométrie (voir la cartographie, métrologie, architecture);
Le nombre qui se déploie dans le temps, c'est la musique, l'harmonie, la vibration;
Le nombre qui se déploie dans l'espace et le temps, c'est l'astronomie.
Approfondissons dans ce chapitre l'astronomie.
Un certain nombre de chercheurs ont pu mettre en évidence des rapports de nombre avec les astres. Observer un lever de soleil, c'est de l'astronomie. Observer la lune, c'est de l'astronomie.
Quand j'explique que je fais de l'astronomie, on a tendance à me demander la marque de mon téléscope, et la taille de l'engin......
Aucun engin n'est nécessaire pour faire de l'astronomie au sens des anciens. Mais cependant, il faut reconnaître qu'un certain nombre d'indices amènent à penser que les anciens pouvaient voir de manière distante, avec des instruments.
Dans cette partie, vous verrez comment:
Vénus, diamètre et distance au soleil, est encodée dans la tour ronde du château des Allymes;
Soleil, diamètre solaire, est encodé dans le plan modulaire carré 5×11 du château des Allymes;
Terre, diamètre volumétrique moyen et distance au soleil, est encodée dans le plan modulaire carré, dans l'enceinte principale carrée, et dans la tour ronde.
Lune, diamètre lunaire, dans le plan modulaire carré;
1. Vénus et la tour ronde
Le lecteur pourra regarder la partie métrologie, ainsi que la partie cartographie pour comprendre ce qu'il va suivre.
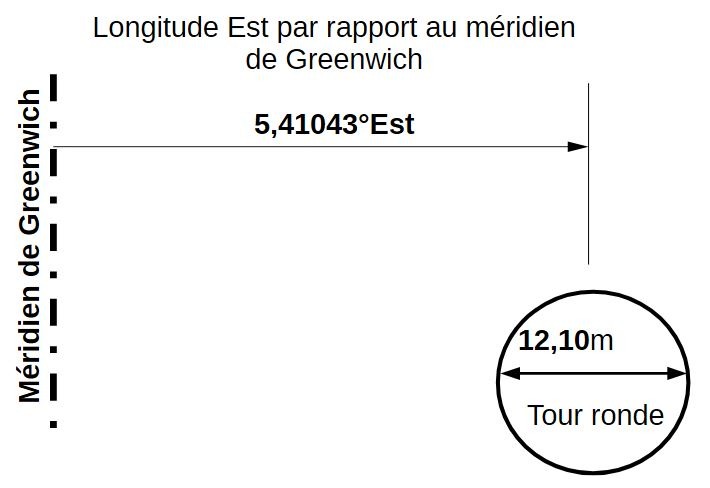
Deux attributs importants de la tour ronde:
Son diamètre de 12,1m exactement;
elle est à la longitude de 5,41043° Est. La référence par rapport au méridien de greenwich.
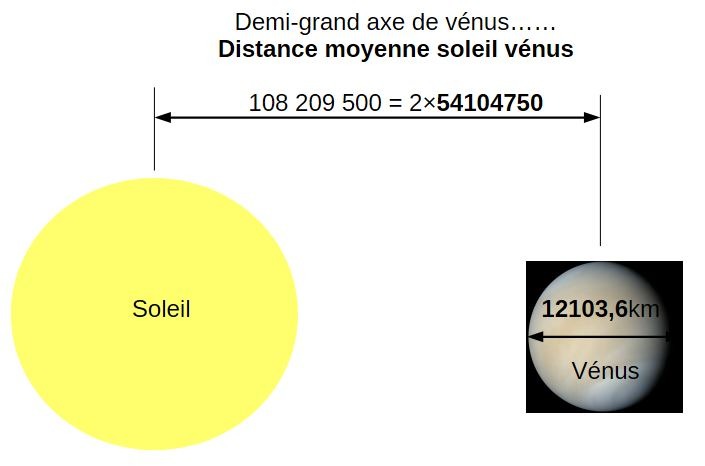
Deux attributs importants de la planète vénus:
son diamètre de 12103,6km;
sa distance au soleil de 108209500. La référence est le centre du soleil lui-même.
Voilà. Nous avons une référence objective pour positionner un centre, et le diamètre de l'objet considéré. On voit que les valeurs sont quasiment égales.
Deux remarques s'imposent:
Vénus est la planète la plus sphérique du système solaire. Son diamètre équatorial est à peu près le même que le diamètre méridional;
Vénus est la planète dont l'orbite est la moins elliptique du système solaire. C'est donc la plus circulaire.
Vénus a donc ses deux paramètres les plus importants pour la décrire, qui sont par ailleurs les plus parfaits du système solaire.
Quels pourraient être les deux paramètres suivants par ordre d'importance?
Disons le d'emblée:
la période de révolution sidérale: c'est le temps que met Vénus à faire le tour du soleil pour revenir à sa même position, soit 224,667 jours terrestres;
la période de révolution synodique: c'est le temps que Vénus reviennent à la même place dans sa configuration Terre Soleil Vénus, soit 583,92 jours terrestres.
On peut donc ainsi mettre en équation Vénus et la tour ronde par leurs propriétés intrinsèques en équation:


On peut voir que cette équation est remarquable pour la tour ronde et sa position sur terre (cartographique). Cependant l'équation est moins précise pour vénus. En effet, j'ai arrondi aux 3 premiers chiffres significatifs la période de révolution à 224 au lieu de 224,667. La période synodique arrondie à 584 s'entend très bien par contre. Mais globalement, on a une expression des deux objets Vénus et tour ronde à peu près en conjonction.
Enfin, on retrouve la latitude, au sein même du plan modulaire carré avec les nombres 119 et 11.
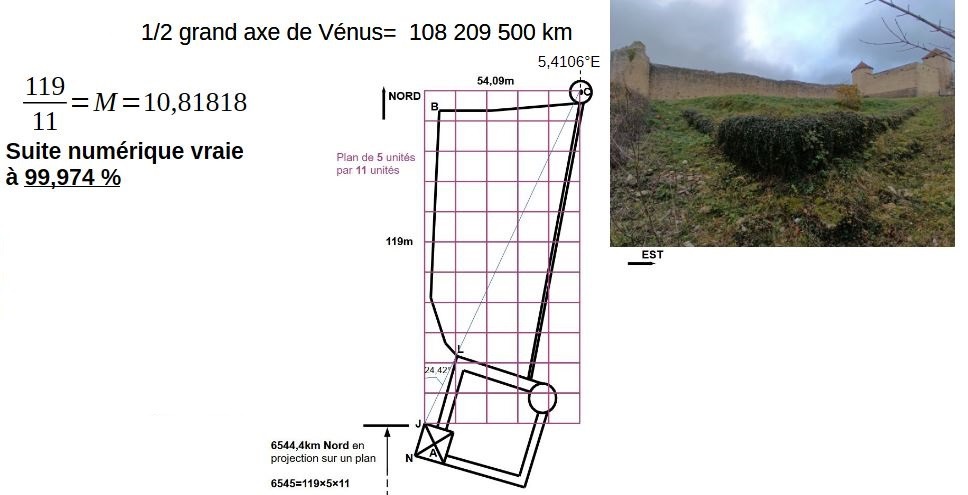



2. Le soleil
Autant le dire d'emblée, la mise en volume de certains éléments de surface nous donne très précisément la valeur du diamètre du soleil: 1392684km
On peut faire ceci sur:
le plan modulaire carré de 5×11;
La tour ronde;
en partie seulement, sur la tour carrée;
Pour la tour carrée, nous allons voir qu'elle est liée à la tour ronde, mais sur le même principe.
C'est un principe de base de la construction du château par les nombres.
On remarque que la distance linéaire de 117m entre J et K est égale en nombre (pas en unité) à la surface d'un petit module carré 117m² . Or, le point K n'étant pas lié géométriquement au plan modulaire carré, il est cependant lié à celui-ci par le nombre. Mettons cette superficie de 117m² en volume pour en faire un cube.
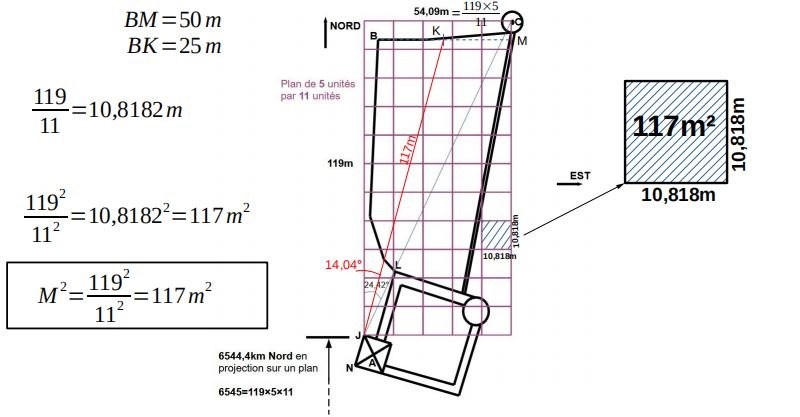
Prenons le plan modulaire carré. Chaque module carré fait 119/11=10,818m de coté. Sa superficie fait donc 117m². c'est à dire 119²/11².
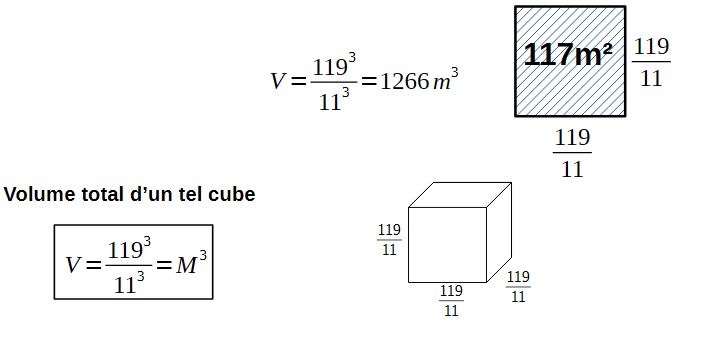
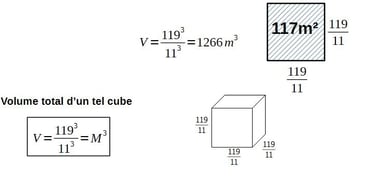
Nous avons 55 cubes sur le plan modulaire carré, donc:
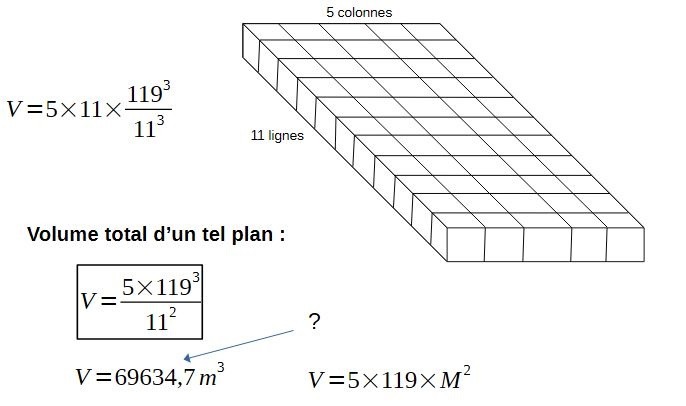
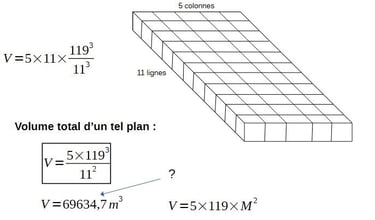
Que représente ce nombre?
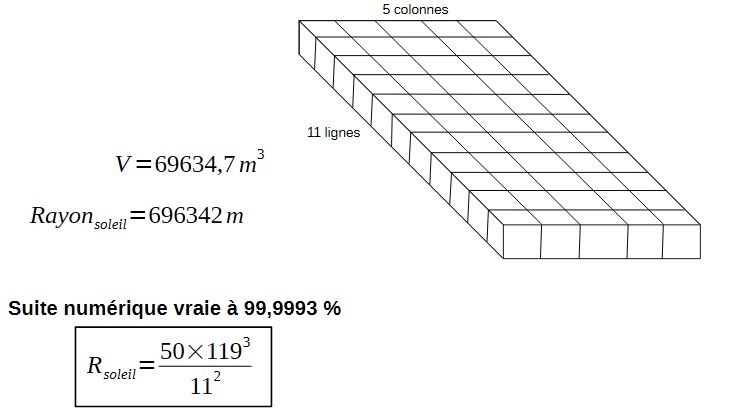
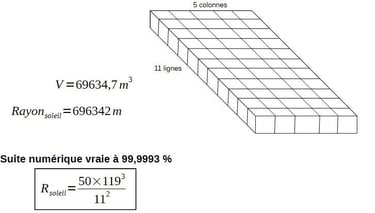
Nous avons ici le rayon du soleil, avec une précision absolument extrême.
Donc, il faut deux étages à ce plan modulaire carré pour obtenir le diamètre solaire:
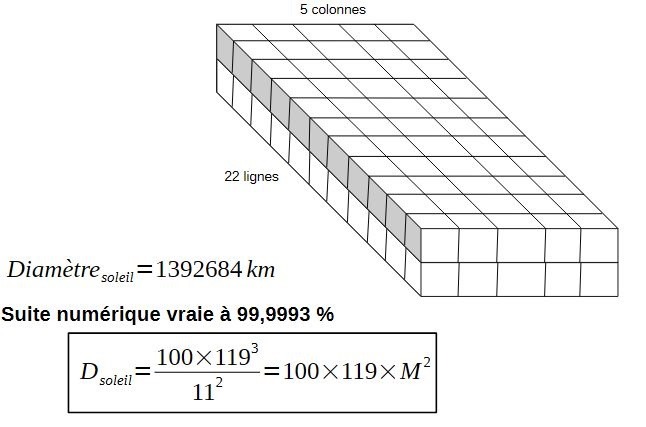
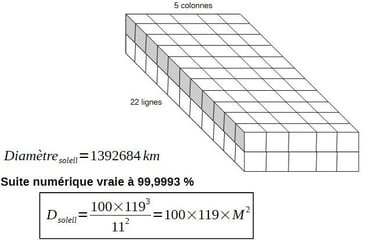
Au-delà du côté spectaculaire de la précision, nous avons maintenant des nombres pour donner une fraction exacte au diamètre solaire. Les nombres 119 et 11 sont donc à la racine du nombre solaire. Au passage, rappelons que 119= 7×17.
Mais où cela devient encore plus intéressant, c'est que l'on peut faire la même chose pour la tour ronde qui est, nous le rappelons, associée à Vénus.
Prenons la suite numérique du diamètre de Vénus pour diamètre de la tour ronde: 12,1036 mètres.
Faisons la superficie de ce disque.
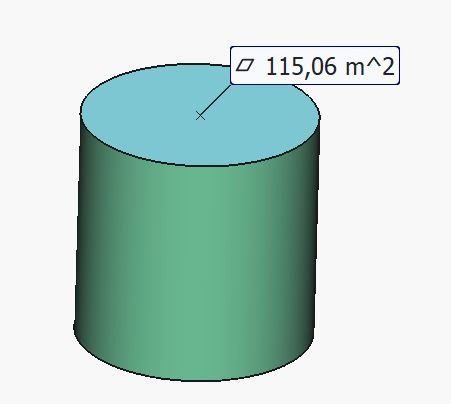
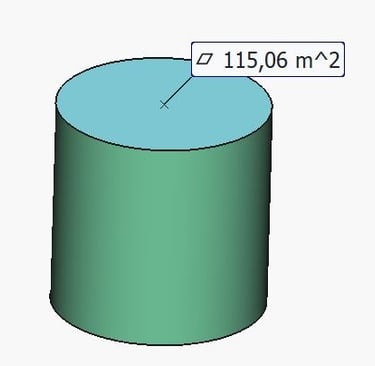
Et maintenant procédons de la même manière que le plan modulaire carré en multipliant par la hauteur qui sera égale au diamètre. On appelle ceci un cylindre équilatéral.


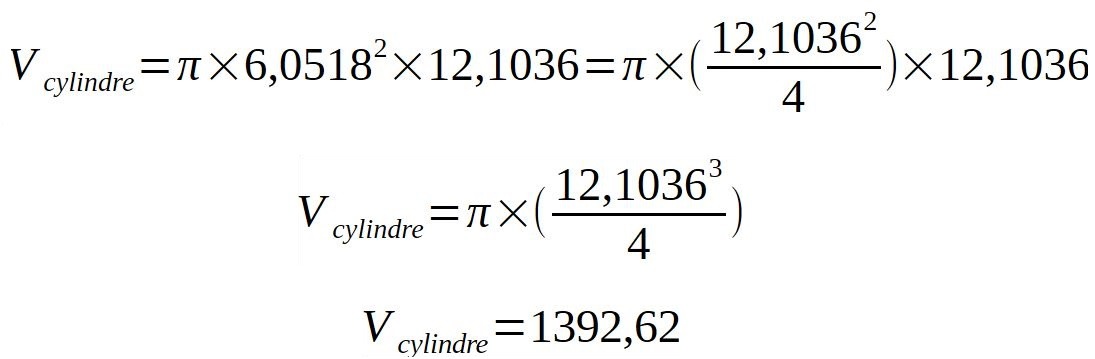
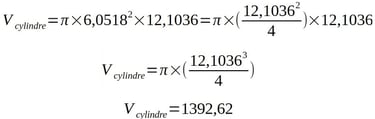
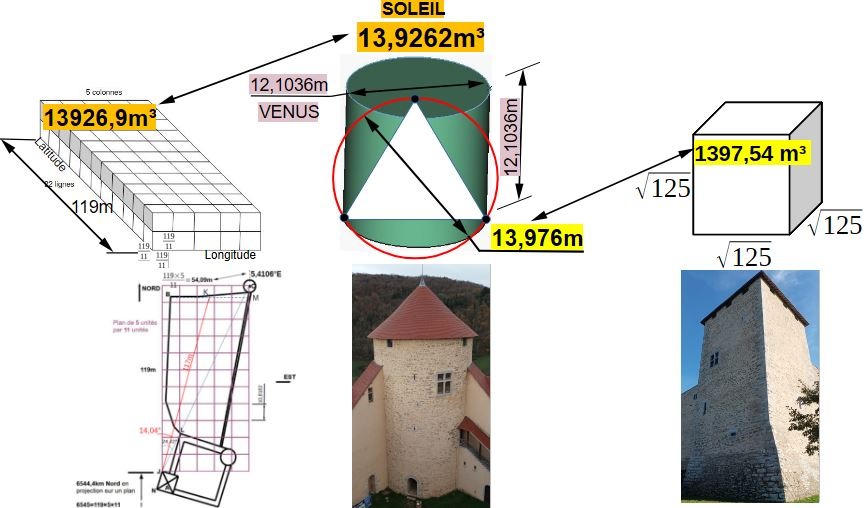
Et voilà. Le soleil a pour suite de nombres: 1392684. Ici nous avons 139262. Nous avons ici le diamètre solaire vrai à 99,995%. Nous partons du diamètre de vénus et nous le mettons en volume, là où nous mettions précédemment en volume le plan modulaire carré, donc partant des latitudes et longitudes terrestres.
Et si nous faisions pareil pour la tour carrée?
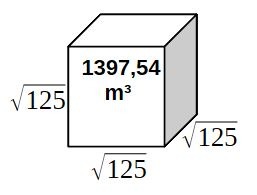
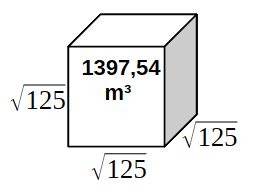
Dans ce cas, nous sommes beaucoup moins précis, mais cela semble marcher aussi. Cette fois nous génèrerons donc un cube.
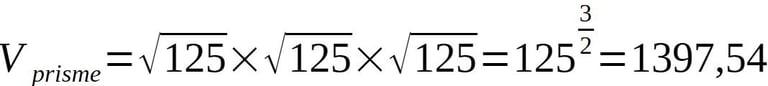
Nous avons donc un diamètre solaire plus approximatif que précédemment. Mais d'ailleurs, cela tombe assez bien, le côté de la tour carrée est lui aussi approximatif. Nous tenons bien une diagonale de racine de 250. Mais la valeur des côtés au dernier étage est "flottante".
Nous pouvons aussi recalculer la valeur cible du côté pour voir combien il faudrait pour atteindre une valeur exacte pour le soleil.
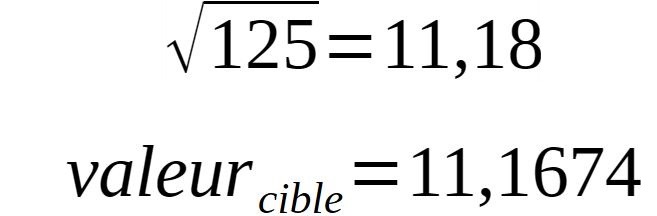
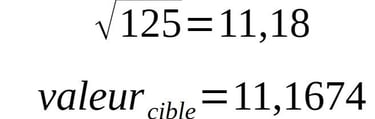
L'écart est en effet très grand sur la valeur en volume, mais finalement, sur la valeur racine, il n'y a qu'un cm d'écart sur 11m.... qui se répercute grandement car mis au cube.
Le principe marche donc aussi pour la tour carrée, car nous tenons les 3 premiers chiffres significatifs. Cependant, cette erreur doit nous amener à nous questionner, en effet, nous avons l'habitude d'une grande précision. Nous allons voir que la réponse se trouve, une nouvelle fois, dans la tour ronde.
La valeur de la mise au cube du côté du carré vaut la suite numérique de 139754.
Mais arrêtons nous un instant sur cette mise au cube de la racine de 125.
Combien vaut le côté de ce volume? racine de 125. Or, la racine de 125, c'est la racine du nombre 5 mis au cube.......
Et donc nous avons le nombre 5 qui est mis en puissance:
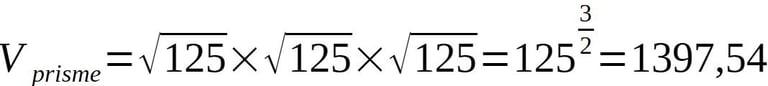
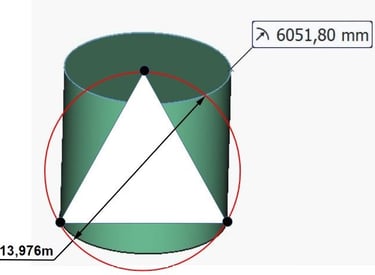
Reprenons le cylindre équilatéral de la tour ronde. C'est à dire la hauteur sera égale au diamètre, c'est à dire 12,1036m.
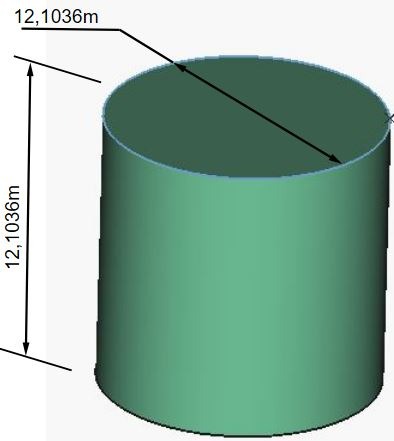
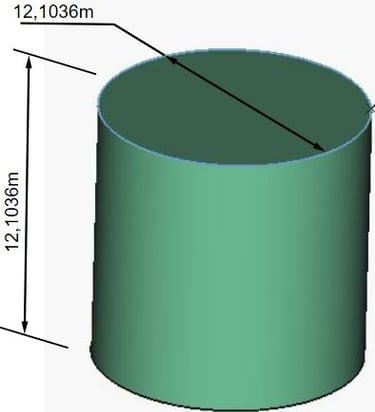
Ce volume, avons nous dit, vaut très précisément la suite numérique correspondant au diamètre du soleil.
Traçons le triangle équilatéral issu de cette figure, les trois côtés valant 12,1036. La hauteur de ce triangle est égale à 10,482m.


Traçons le cercle qui inscrit le triangle équilatéral:
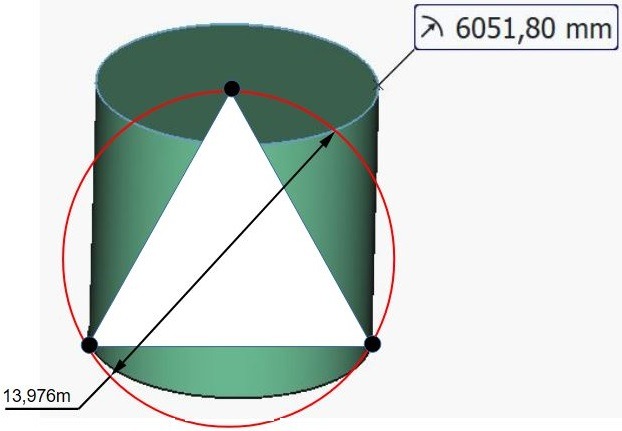
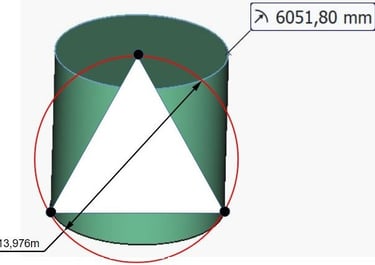
Nous avons donc un diamètre de 13,976m qui inscrit ce triangle équilatéral vertical.
Or, le volume total de la mise au cube du côté du carré de la tour carrée vaut la suite numérique de 1397,54.
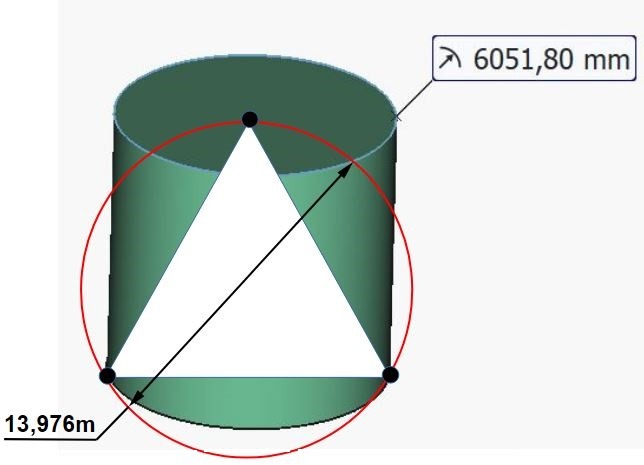
Et oui, le côté du carré est déjà une mise au cube de la racine de 5.
Donc, le côté du carré de la tour carrée est "déjà" un cube de racine de 5 de côté.
Et par conséquent, le volume total est un cube du cube de la racine de 5. Le nombre qui en est issu inscrit le triangle équilatéral du volume cylindre équilatéral issu de la tour ronde....donc du nombre du soleil.
La racine de 5 est constitutive du nombre d'or et inscrit le diamètre du soleil dans un cercle dont le triangle équilatéral donne un cylindre équilatéral partant du diamètre de vénus exactement.
Comment ont-ils mesuré les diamètres de vénus et du soleil? toute réponse à ce sujet est une hypothèse dont on ne peut actuellement pas démontrer la véracité.
Nous pouvons cependant montrer par analyse géométrique et numérique que cela a existé au XIVe siècle.
Nous pouvons aussi donner des explications à POURQUOI cela:
Une volonté de mettre en volume par la hauteur pour se rapprocher du brillant, du solaire. La hauteur est le soleil. La surface au sol est terrestre ou vénusien au château des Allymes, une volonté de se rapprocher de l'irrationalité de l'univers et de l'ordonner sur terre;
Une volonté de lier le plan modulaire, la tour carrée et la tour ronde PAR le Soleil. Une recherche donc de lier les structures, et de les ordonner PAR ce qui est le plus brillant.
Une volonté d'inter-mélanger le soleil et Vénus. Vénus est inscrite dans le soleil. Le soleil est porteur de Vénus. Une volonté de réunir Vénus ET le Soleil, au sein de la tour ronde, c'est à dire Vénus. L'ordre géométrique par la racine de 5 permet de remonter ET au diamètre solaire ET au diamètre Vénusien TRES EXACTEMENT.
La racine de 5, partie irrationnelle du nombre d'or, à travers la tour carrée, se suffit à elle même. Le solaire se suffit à lui même. Vénus a donc besoin du Soleil. Ce qui, astronomiquement parlant, est tout à fait exact.
Le plan modulaire carré, véritable géolocalisation du site, est mis en hauteur vers le soleil. Nous réunissons ici la terre et le ciel. Nous attendons les conclusions des historiens et archéologues sur ce que contenait ce plan modulaire carré. Certains disent qu'un village devait être là, mais malgré la réalisation de tranchées dans ce plan, aucune construction n'a été retrouvé encore.....à suivre.
En résumé:
Le plan modulaire carré est une géolocalisation terrestre. Si on en fait un volume (vers le haut), on obtient le diamètre solaire;
La tour ronde possède tous les attributs de vénus. Si on la met en volume en cylindre équilatéral, elle nous donne le diamètre solaire;
La tour carrée a un côté de racine de 125. Un nombre solaire lié au nombre d'or par la racine de 5. Mis en volume, nous avons le diamètre du soleil, grossièrement. Mais nous avons surtout la suite numérique du cercle qui inscrit le triangle équilatéral de la tour ronde.
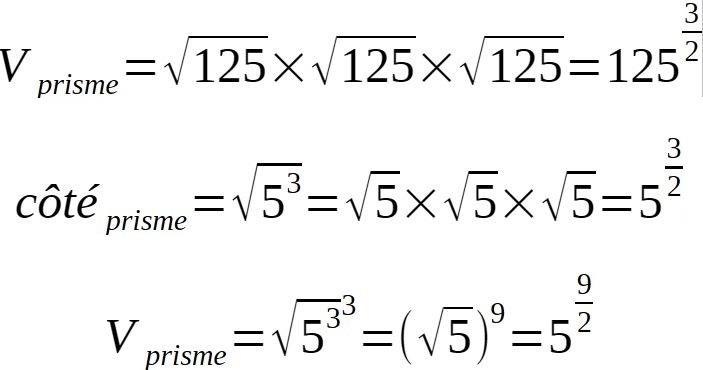
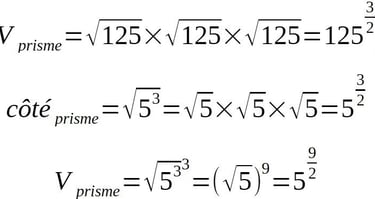
3. La Terre
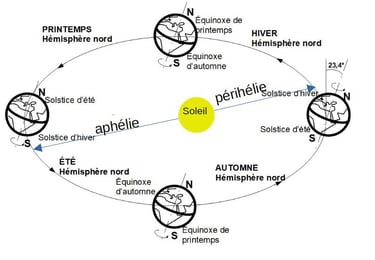
Dans ce travail astronomique, peut-on retrouver les paramètres astronomiques de la planète Terre?
Pour la Terre, on appellera paramètre astronomique les paramètres qui ne dépendent pas de la géométrie terrestre. Rappel: géométrie vient de mesure de la terre.
Nous avons trois paramètres astronomiques évidents:
Le diamètre volumétrique moyen: c’est le diamètre de la sphère qui aurait le même volume que la Terre réelle (qui est légèrement aplatie aux pôles). Le diamètre volumétrique de la terre = 12742,016 km. Ce diamètre ne tient pas compte de l'aplatissement, donc, des coordonnées géographique. C'est un diamètre qui est utile en astronomie moderne pour comparer des planètes entre elles;
La période de révolution autour du soleil: 365,256363 jours terrestres pour revenir à la même place;
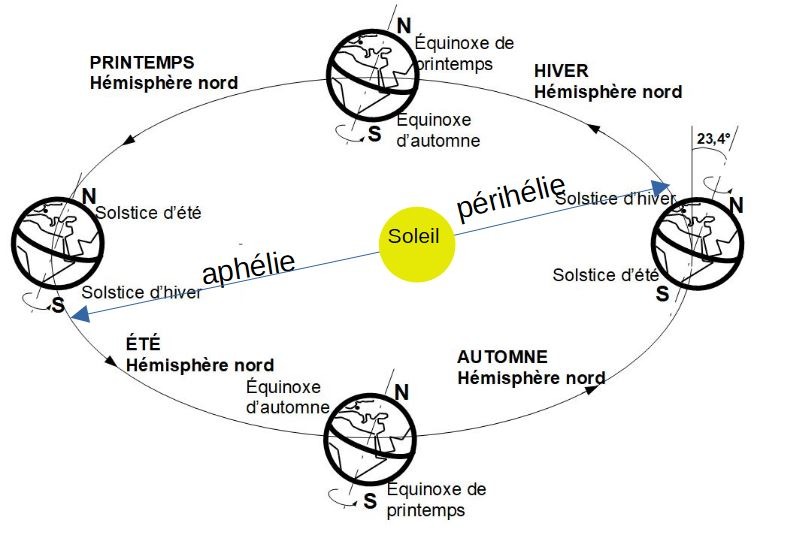
La distance Terre- Soleil moyenne: c'est ce qu'on appelle le demi-grand-axe, et il vaut 149 597 887,5 km. En fait, la terre tourne de manière elliptique déplacée autour du soleil. La terre est donc au plus près du soleil vers le solstice d'hiver (périhélie, 147 098 074km), et au plus loin du soleil vers le solstice d'été (aphélie, 152 097 701km). Le demi grand-axe est donc la distance moyenne au soleil, comme si la terre faisait un cercle parfait autour du soleil.
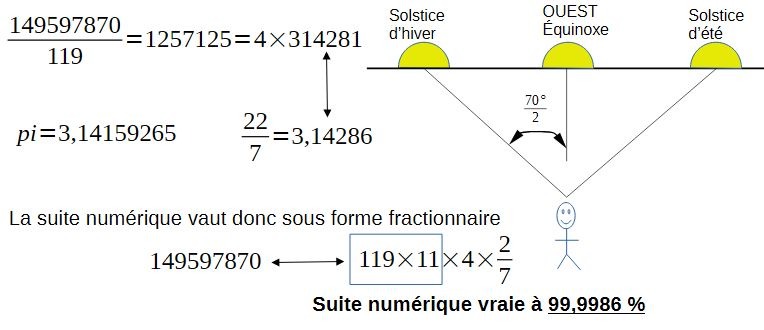
La suite numérique vaut donc sous forme fractionnaire:
Et l'on voit de nouveau apparaitre le 11 dans cette suite. Il serait aisé de faire apparaître le 5 aussi pour revenir au plan modulaire carré de 5×11. La fraction 22/7=3,142857 est typique de la fraction représentant pi dans le monde antique ou bien chez les égyptiens.
On observe qu'apparait la fraction 2/7 dans cette équation du demi grand-axe Terre-Soleil. A Ambérieu-en-Bugey, de latitude 45,958°Nord, nous avons un demi-angle solsticial de 35° à peu près exactement.
Or, 2/7=0,35. Nous n'allons pas tout expliquer ici, mais cette suite 35 se retrouve dans le rapport de la terre au soleil sur les levers maximum aux couchers de soleil des solstices.
Cette mise en fraction va donc plus loin, sur le plan astronomique à Ambérieu-en-Bugey, que simplement le demi grand-axe.
A noter que si l'on prend la valeur irrationnelle de pi, nous nous écartons de l'exactitude précédente. C'est donc par la fraction de 22/7 que l'on arrive ET à l'exactitude, ET au nombre 11 renvoyant au plan modulaire carré, ET à la fraction 2/7 renvoyant à la suite numérique 35 caractéristique du demi-angle solsticial.
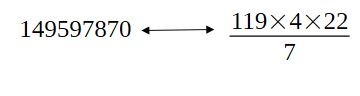
Reprenons l’idée de la division par 119, que l'on a déjà vue car issue du plan modulaire carré 5×11.
1/2 grand axe terre/soleil=149 597 870km.
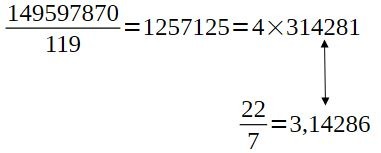
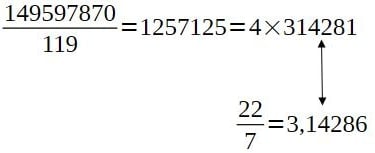
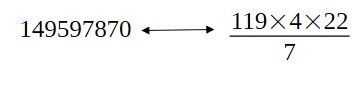
Constatations:
Se placer en J et regarder le point C (déjà implanté dans un autre article) permet de positionner L angle des courtines NORD-OUEST. L'angle de 24,42°N correspond à la diagonale d'un rectangle de 5 par 11 orienté plein nord dans sa grande longueur. Les points J, C et L sont alignés. Ici les nombres ne sont pas étonnants. 130,8 c'est 2 fois le 65,4, que l'on a pu observer maintes fois entre Tour de Saint-Denis vers château des Allymes (voir cartographie2).
La distance JL vaut environ 26m, mais difficile à mesurer précisément. JL≈ JC/5
Mais il y a quelque chose de plus dans cette géométrie, c'est le jeu entre le 11 et le 119 pour engendrer un rejeton du nombre d'or.
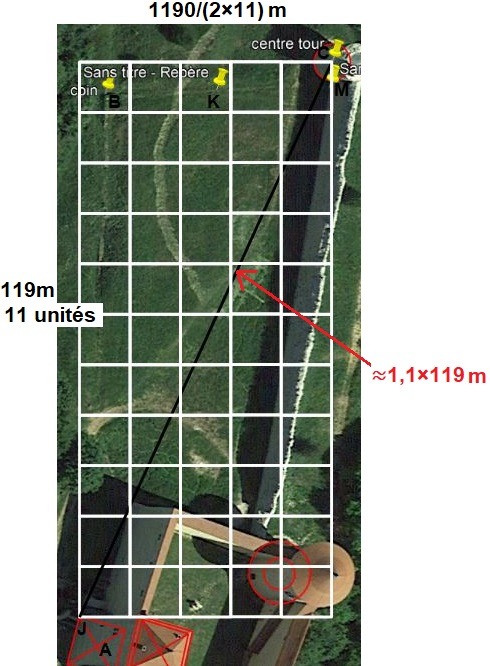
Le côté de 11 unités de la géométrie fait 119m.
Le côté de 5 unités de la géométrie fait 1190/ (2×11)m.
Mais 130,8 ≈ 1,1×119. Et le nombre d'or au carré divisé par 2 = 1309. Avec les modules de 5×11 avec le 119 de côté 11, nous obtenons une diagonale signifiante du nombre d'or au carré/2.
Chacun des côtés du triangle JRC possède une relation aux nombres 119 et 11. 11 et 119 forment le nombre d'or à leur manière dans la géométrie modulaire carrée de 5 par 11!
4. Comment la tour ronde nord est-elle positionnée?
Nous avons vu que AB= 120m exactement, et orienté plein nord.
Partons de J et allons plein nord en R. Recoupons avec un axe EST-OUEST pour revenir au point C, centre de la tour ronde Nord.


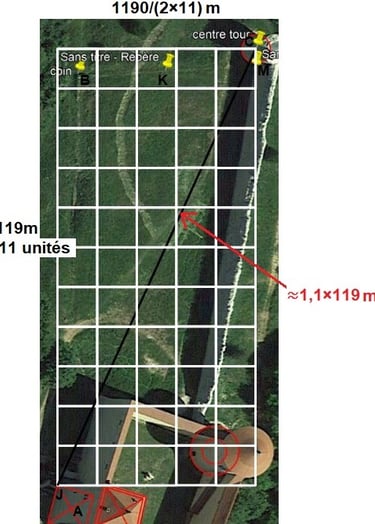
En conclusion, du point de vue de l'arpenteur-géomètre médiéval, se placer au point J de la tour carrée permet de positionner précisément le centre de la tour ronde avec une géométrie modulaire mesurable, dont les nombres indiquent leur importance dans la construction, et faisant ressortir un nombre bien connu au moyen âge: le nombre d'or.
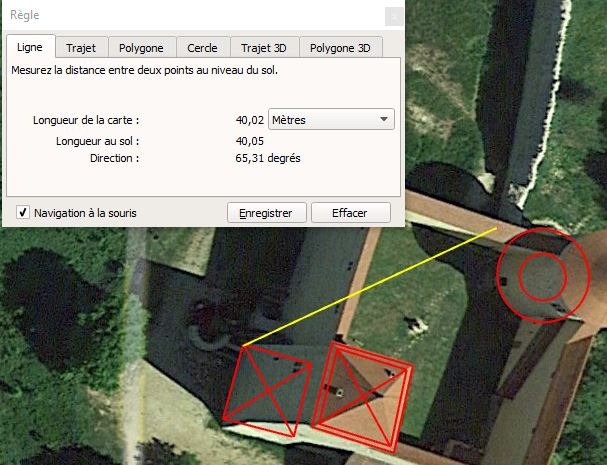
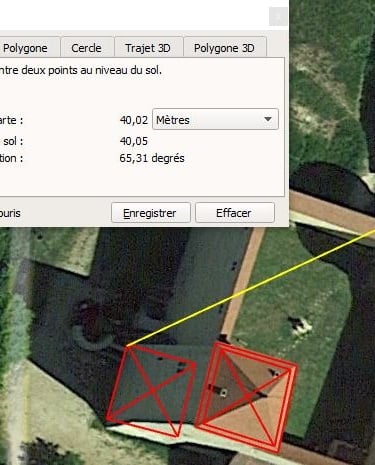
Enfin ce mur peut être positionné à 40m et 65,3°N environ depuis l'angle de la tour "carrée".
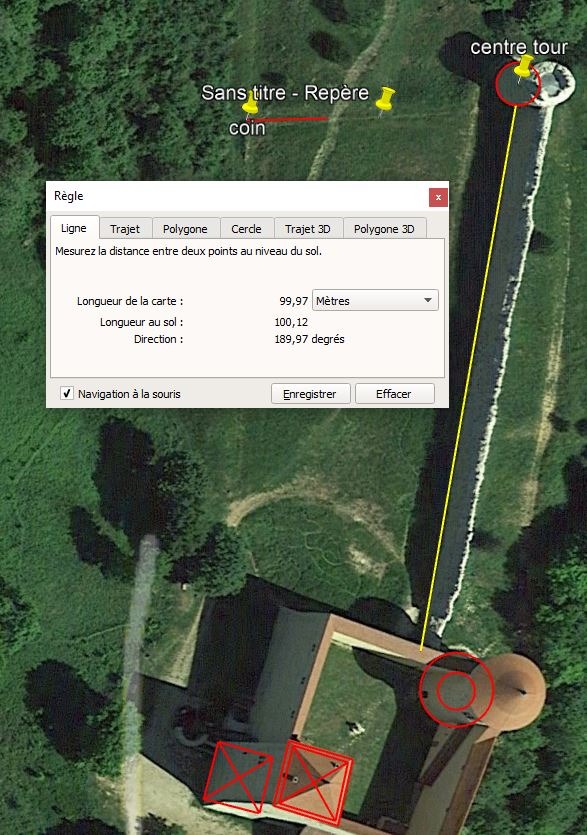
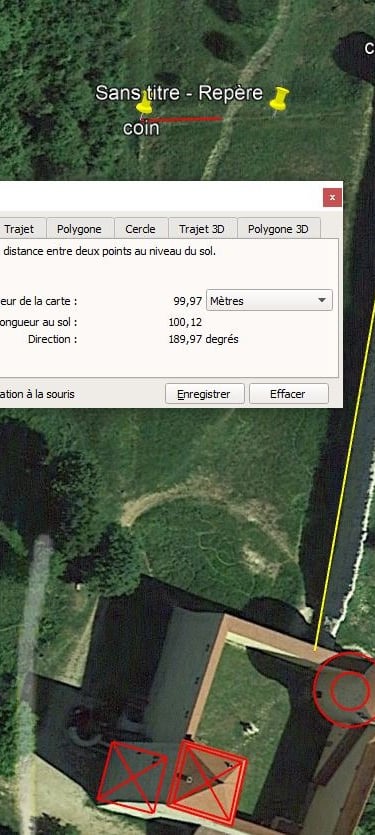
Autre remarque: Le grand mur est orienté à 10°N et fait exactement 100m. Je tiens compte de l'épaisseur de la courtine du château pour cette mesure sur GE pro. Le relevé des archéologues¹ montre la même mesure.
Conclusion
L'angle J de la tour rectangulaire du château des Allymes joue un rôle très important dans l'implantation des parties annexes comme les murailles annexes. Il place aussi la courtine de 36m de côté, notamment à cause de la relation d'alignement entre les points J, L et C. Il place aussi la muraille de 100m de long.
Il reste la question de l'infléchissement de la muraille légère au Nord. pourquoi avoir changé l'angle et ne pas avoir gardé une trajectoire plein Ouest? à 1m ou 1m 50, cela n'aurait certainement pas changé grand chose. Cependant, ils l'ont fait.
Sources:
¹. Des bâties de bois aux bâties de pierre - Laurent d'Agostino - Rediffusion Bastida, Culture.Isère: https://www.youtube.com/watch?v=JtJq-AbOj3U, à 1h10' 44'', 2022
